こんにちは,madoryです!
本時より新しい単元【図形と計量】の学習をスタートします

レッサーくん!!
富士山の高さって覚えてる?

もちろん!『3776m』だよ!!
ぼくが住んでる日本平動物園から見えるもんね♬

じゃあ,富士山の高さが3776mであることは,
どうやって確認できると思う??

えっ……。
そう言われてみればどうやって測るんだろう…?
突然ですが,あなたに質問です!!
「富士山の高さは 3776mですが,どうやって富士山の高さを測りますか??」

3776mもの高さの場所まで行って,まっすぐ標高 0mまでメジャーを垂らす…
当然そんなことできやしません!!
そこで,本単元【図形と計量】で学習する❝三角比❞の登場です!
❝三角比❞という新しい考え方を利用して図形を考えていくことで,様々な長さや高さ,角度の計量(いわゆる測量)ができるようになります
その第1弾として,本時では三角比の定義について理解していきましょう!

三角比を利用すると,
メジャーを使わなくても色んな長さが測れるようになるんだ♬

三角比って何だかすごそう!!
勉強するのがワクワクしてきたよ♬
さっそく本時の結論です
三角比の定義は,3つの暗記方法から選択せよ!
三角比の定義とは?
直角三角形において,角度の1つを θ とします
斜辺の長さをr,横の長さをx,縦の長さをyとするとき,
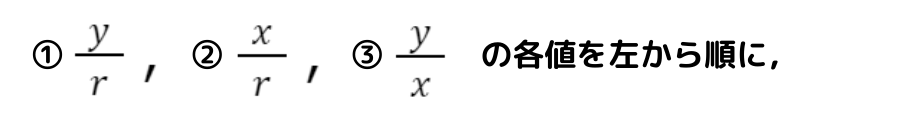
- 正弦(sine:サイン)
- 余弦(cosine:コサイン)
- 正接(tangent:タンジェント)
といい,
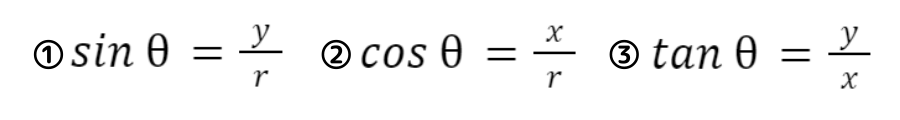
と書きます
三角比とは,サイン(sine)・コサイン(cosine)・タンジェント(tangent)の総称です

なんだかとってもややこしい…

「サイン」「コサイン」「タンジェント」と
何度も言って慣れようね♬
これらを簡単にまとめると次のようになります
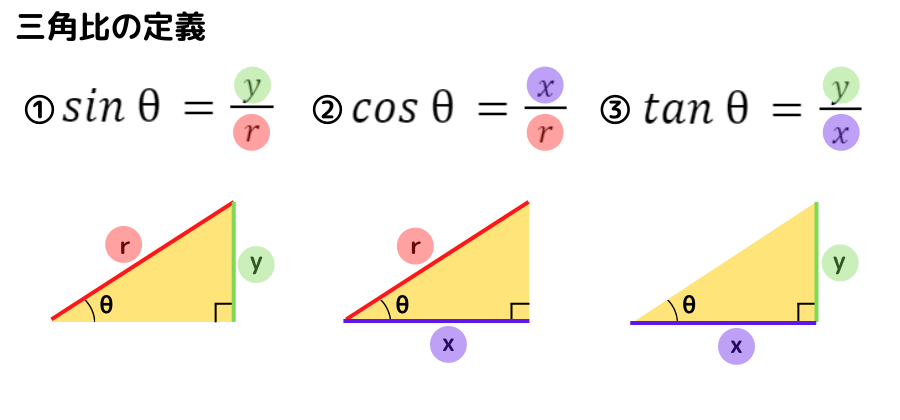

直角三角形の2辺を選んで分母・分子にするんだね!
どの2辺を選ぶのか間違えそうだ……。

そうだね!
他にも,分母と分子を逆に書いてしまうこともミスとしてよく起こるよ!!
そうならないための暗記方法があるんだ♬
暗記方法1:s,c,tの筆記体
まず1つ目の暗記方法を紹介します
サイン(sine)・コサイン(cosine)・タンジェント(tangent)の頭文字である『s,c,t』の筆記体を図形に当てはめる方法です!

筆記体なんて学校で習わないし知らないよ~。

s,c,tの3つだけは筆記体を覚えておこうね!
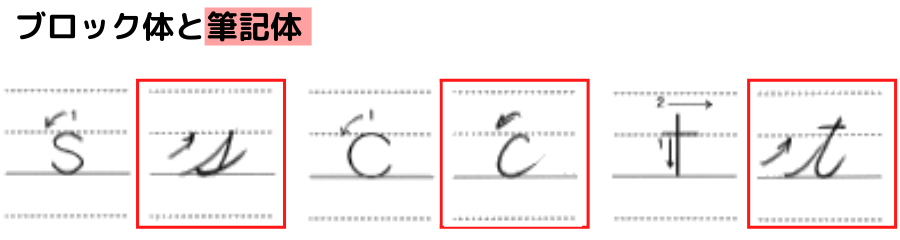
この筆記体を三角比の定義に当てはめます
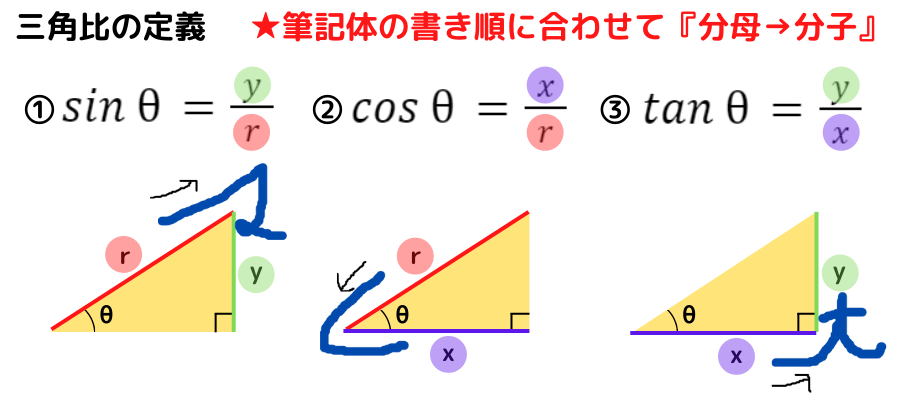

まず直角三角形の2辺に筆記体を合わせるよ!
次にそれぞれの書き順に合わせて『分母→分子』を作るんだ!

おー!!筆記体を覚えれば定義が作れるんだね♬

直角三角形を置く向きも大事になるよ
『直角を右下』『 θ を左下』に置こうね!
上記の図のように,まず筆記体を直角三角形の2辺に合わせるように書き,次に書き順に合わせて『分母→分子』を作ります
三角比の定義の暗記方法として,最もポピュラーな方法です!
また,筆記体を使用して暗記する場合,直角三角形を置く向きも大事になります
『直角を右下』『 θ を左下』に置くようにしましょう!
直角三角形を置く向きがズレると,辺の場所が異なってしまうため注意が必要です!!
暗記方法2:色分けして一周回す
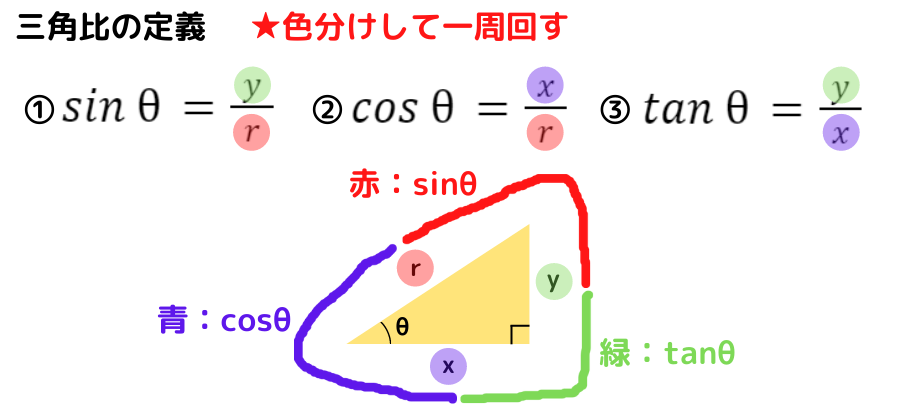

一周ぐるっと回すように書いて覚える方法だよ!
色分けすることでイメージしやすくなるね♬

どの2辺を用いる三角比なのか分かりやすいね!
分母と分子がどちらの辺になるかは覚え方には入ってないから注意だね‼
こちらは視覚的に理解したい人におすすめの方法です♬
どの2辺がサイン・コサイン・タンジェントなのかが分かりやすいです
ただし,分母と分子がどちらの辺になるかは分からない覚え方なので,その点は注意です!
暗記方法3:さるわコルクたくわん
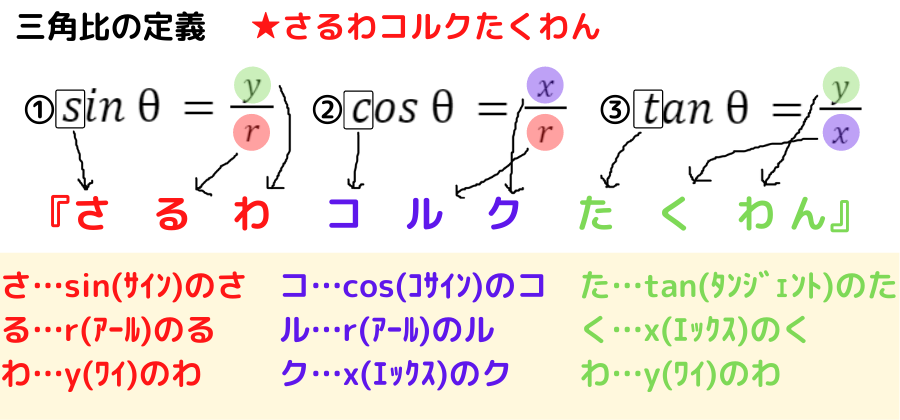

語呂合わせで覚える方法を紹介するね!
分母→分子の順に語呂合わせで覚えられるよ♬

ぼくはこの語呂合わせが一番覚えやすいな♬
3つ目は語呂合わせで覚える方法です
「三角比の名称→分母→分子」の順に進むように,本時の授業のために作ってみました!
いかがでしょうか?
もし覚えやすいように感じてもらえれば,こちらの語呂合わせで覚えてみてくださいね♬
★補足★ 実は三角比の定義は教科書によって違う?!

そういえば…中学校で三平方(ピタゴラス)の定理を勉強したとき,
直角三角形の3辺は「x, y, r」でなくて「a, b, c」で習った気がするな…。

よく覚えていたね!その通り‼
高校の別の教科書によっては「a, b, c」を用いるものもあるんだよ。
本時の授業では,直角三角形の3辺を「x, y, r」で紹介しましたが,あなたの高校では「a, b, c」で書かれているかもしれません!!
実は,三角比の定義は教科書によって書き方が異なるのです!!
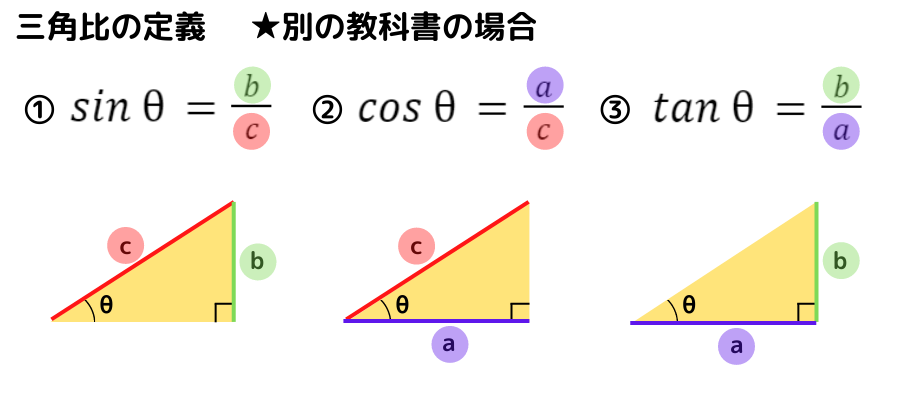

ぼくは「a, b, c」の方に慣れているからこっちがいいのになぁ~。
なんで教科書によって書き方が違うんだろう…??

三角比の定義としては,どちらも同じ意味のことを紹介しているんだよ!

なんで教科書によって書き方が違うのか…。
その理由を教えるね!!
「x, y, r」でも「a, b, c」でも三角比の定義の意味は同じです
ではなぜ使用する記号が異なるのか…
「x, y, r」を使用するメリット・デメリットは次の通りです!
【メリット】
・「図形と計量」の単元の学習が進むと「x, y, r」で三角比の定義を覚える必要があるため,新たに三角比の定義を覚え直す必要がない
【デメリット】
・中学校で「a, b, c」を使用するから「x, y, r」の記号に馴染みがなく,三角比の定義を覚えづらく抵抗を感じやすい
・問題文では直角三角形 ABC を用いるため,辺の長さは「a, b, c」で表すことが多く,「x, y, r」の記号と結びつきづらい
一方,「a, b, c」を用いるメリット・デメリットはその反対になります
【メリット】
・中学校で学習した記号と同じであるため受け入れやすく,定義を理解しやすい
・問題で三角形 ABC を用いるため,辺の長さをそのまま「a, b, c」として認識しやすい
【デメリット】
・「図形と計量」の単元の学習が進むと,「x, y, r」で三角比の定義を新たに覚え直す必要がある
どちらの表現方法にも良さがあることがお分かりいただけたでしょうか?
あなたの高校の教科書はどちらの表現方法になっているのか…
調べてみると面白いですね♬
それでは本時のまとめです
- 三角比の定義は直角三角形の2辺を分母と分子に代入して作られる
- 三角比とは,サイン(sine)・コサイン(cosine)・タンジェント(tangent)の総称
- 三角比の定義を覚える際の直角三角形の置き方は,『直角を右下』『 θ を左下』
- 暗記方法は3つ!①s, c, t の筆記体②ぐるっと一周回す③さるわコルクたくわん
- 教科書によっては,三角比の定義を紹介する際,直角三角形の3辺を「a, b, c」を使用しているものもある
- 「x, y, r」と「a, b, c」,どちらにもメリット・デメリットがある
本単元「図形と計量」は,三角比の定義を覚えることがスタートです!
紹介した3つの暗記方法からお好きな方法を選び,楽しく覚えてくださいね♬
今回は以上です。ありがとうございました
 すうがくの両先生
すうがくの両先生 

