サッカークロス 
こんにちは，madoryです！
レッサーくん!!
三角定規って覚えている？
もちろん覚えているよ！
中学校の数学の授業でずっと使っていたよ♬
じゃあ，『三角定規の三角形の角度』って分かる？
『45°，45°，90°』と…
あれ，もう一つは何だっけ？
中学校では数学の授業で三角定規を使用し，作図を学習してきました
❝垂直二等分線❞や❝角の二等分線❞を引いた記憶があるのではないでしょうか？
本時は，そんな三角定規にまつわるお話です
なんと，
「三角定規には，三角比に関する重要な情報が詰まっているのです！」
本時の授業を通じて，三角定規に関するあなたの❝見方❞がきっと変わることでしょう！
それではさっそく三角定規の秘密を解き明かし，『30°，45°，60°の三角比』について考えていきましょう
まず本時の結論です
30°，45°，60°の三角比は，三角定規を頭の中でイメージせよ！
直定規と三角定規
日常生活でなじみの深い直定規…
一方，中学校の数学でなじみの深い三角定規
三角定規って大きくて形が独特だから，
収納するのに不便だったな～
普段使いなら直定規がいいよね～！
ただ，三角定規には直定規にはない魅力があるんだ♬
直線を引くだけならば，収納力に優れ使い勝手の良い直定規に軍配があがります
直線を引く以外にも機能が詰まっている…それが三角定規です！！
実は三角定規は，三角比を学習する上で欠かせない大事な三角形の形状になっているのです！
まず，三角定規には２種類の形があります
- 30°，60°，90°の直角三角形
- 45°，45°，90°の直角三角形
どのようにして上記の直角三角形ができたのか…
それぞれの直角三角形の作り方について解説していきましょう
30°，60°，90°の直角三角形
30°，60°，90°の直角三角形は次のようにして作ることができます
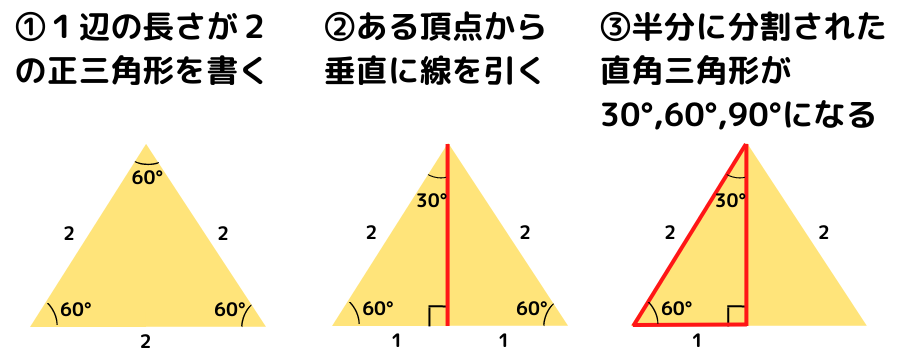
① １辺の長さが２の正三角形を書く
② ある頂点から垂直に線を引く
③ 半分に分割された直角三角形が30°，60°，90°になる
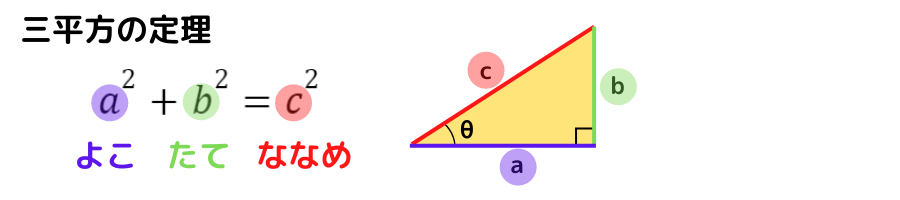
三平方の定理から赤い直角三角形の縦の長さを計算します
三平方の定理って何だっけ？？
直角三角形に成り立つルールで，
別名『ピタゴラスの定理』とも言うんだ♬
45°，45°，90°の直角三角形
45°，45°，90°の直角三角形は次のように作ることができます
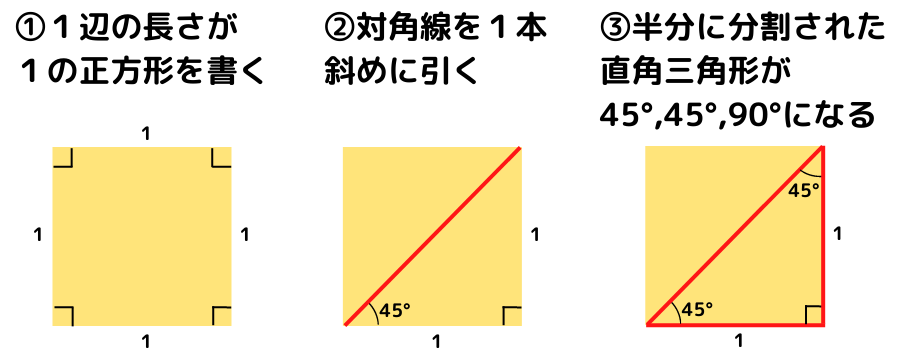
① １辺の長さが１の正方形を書く
② 対角線を１本斜めに引く
③ 半分に分割された直角三角形が45°，45°，90°になる
三平方の定理から赤い直角三角形の斜めの長さを計算します
さっきと同じように三平方の定理を使って計算するよ！
今回は斜めの長さをｘとすればいいね♬
三角定規の辺の長さの比まとめ
レッサーくん，三角定規の秘密が分かったかな？？
辺の長さの比がきれいに求められる特別な直角三角形なんだね！
ここまでを整理してまとめましょう
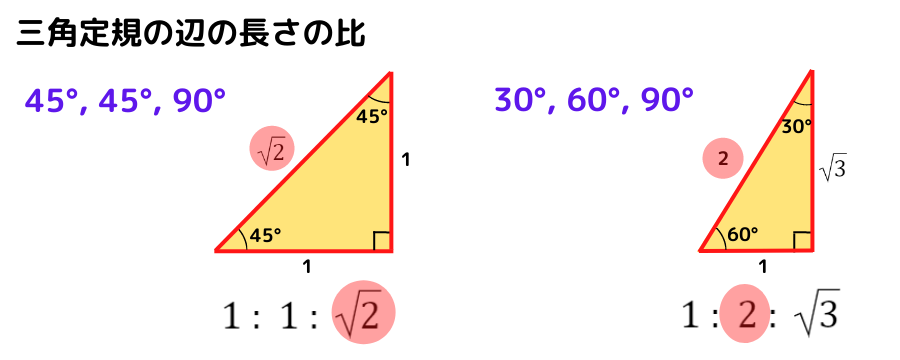
２つの直角三角形で
斜めの長さの比の位置がずれているね！
それは語呂の良さを重視しているからなんだ！
❝最も大きい（長い）値が斜め❞と覚えておこうね♬
上記の２つの直角三角形の辺の長さの比から，三角比を考えていきましょう
三角比の定義については，過去の授業を参考にしてください
【図形と計量①】あなたはどれ派？三角比の定義の暗記方法３選
30°，45°，60°の三角比
まず，30°，45°，60°を左下においた直角三角形を書きます
それぞれの直角三角形において，辺の長さの比から三角比の値を考えていきましょう
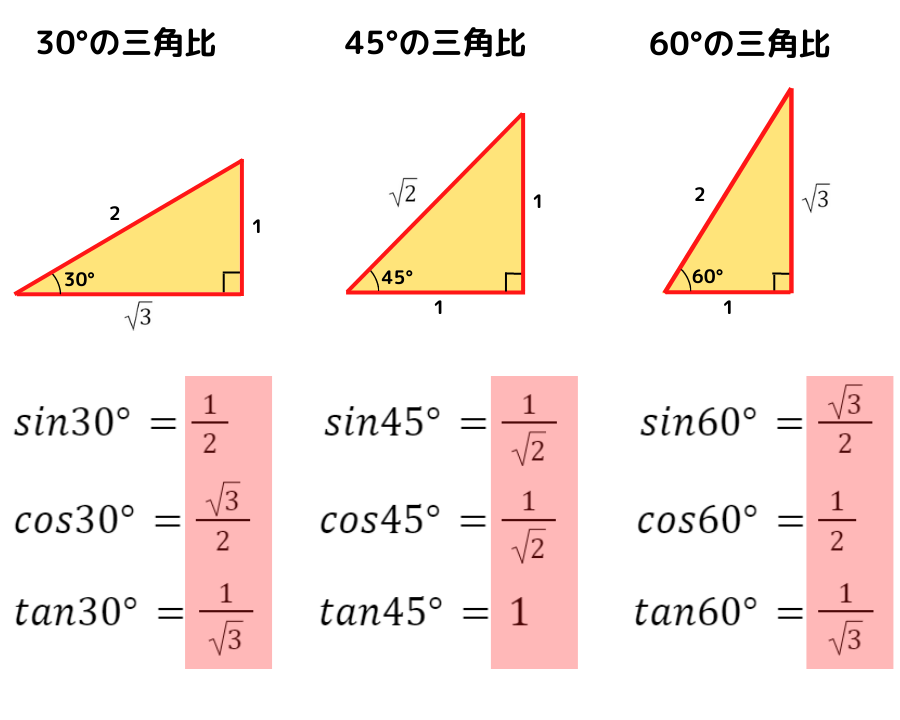
この三角比の値はとっても重要だよ！
すぐに値を答えられるようにしてね!!
★補足★ 三平方の定理の言葉の意味
あなたは，三平方の定理の言葉の意味について考えたことはありますか？
実は『三平方』が定理の中身そのものを表しているのです！！
まず，『平方＝２乗』のことです
面積を求める際に「㎠（平方センチメートル）」という単位を使ってきましたよね？！
このことからも，『平方＝２乗』であることが分かるでしょう
次に，『三平方』の『三』はそのまま数の『３』を表します
まとめると，『三平方＝３つの２乗』なのです！
もう一度改めて，三平方の定理を見てみましょう
『３つの２乗』の定理（公式）であることが確認できましたね！
『三平方』って『３つの２乗』って意味だったんだ！
これでもう忘れないよ!!
それでは本時のまとめです
- 三角定規には『30°，60°，90°』と『45°，45°，90°』の２種類の形がある
- 『30°，60°，90°』の直角三角形は１辺が２の正三角形から作られる
- 『45°，45°，90°』の直角三角形は１辺が１の正方形から作られる
- 三平方の定理を用いることによって，三角定規の三角形の辺の長さの比が決まる
- 30°，45°，60°の三角比は超重要！！
- 三平方の定理の『三平方』とは『３つの２乗』という意味
大きくて不便で，いつもどちらを使うか迷う三角定規…
実は高校数学の授業につながっていたのです！！
これからはあなたの三角定規に対する見方が変わるかもしれませんね♬
三角定規を見た瞬間に『30°，45°，60°の三角比』が連想できる…
そうなってくれると嬉しいです！
今回は以上です。ありがとうございました
