すうがくの両先生 
madoryの『高校数学のブログ授業』です
- 数学を基礎から学び直したい高校生
- 高校入学前に予習して備えたい中学生
- 挫折した高校数学に再挑戦したい社会人
こんな❝あなた❞に向けて発信しています！
さっそく本時の結論です
「平方完成の基本は半分→２乗を引く，応用は係数でくくってから！」
平方完成の目的は，軸の方程式と頂点の座標を求めることです
２次関数の式を，軸の方程式と頂点の座標が分かる形に変形（平方完成）することで，どんな２次関数のグラフでも書くことができるようになります
また，平方完成をすることをすることで，グラフを利用した計算問題に応用していくことができるため，２次関数の単元で平方完成は必須知識です！
本時の授業できちんと押さえておきましょう
それでは結論にしたがって，順番に見ていきます
２次関数のグラフは全部で４種類ありました
厳密に言えば，軸の方程式と頂点の座標が分かる形が４種類でした
詳しくは過去の授業を参考にしてください
【２次関数③】グラフを正確に書く❝５STEP❞
逆に言えば，軸の方程式と頂点の座標が分からない形は，平方完成という式変形をする必要があります
それではさっそく平方完成を行っていきましょう！
平方完成の方法
平方完成の方法は，以下の２つです
- ｘの係数を半分にする
- ①で半分にした値の２乗を引く
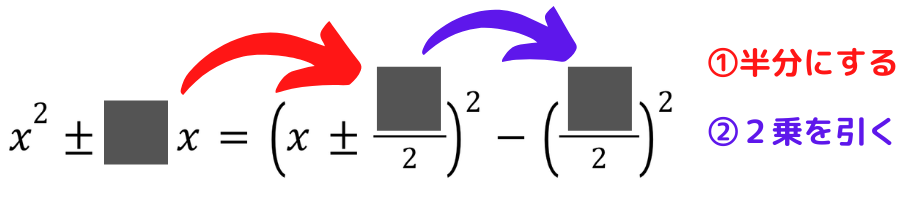
それでは具体例で見ていきましょう！
平方完成の基本 y＝x2＋bx＋c
半分にして２乗を引けばいいから，そんなに難しくないね！
慣れてきたら，暗算して途中計算をとばして，
いきなり答えにいけるといいね！
平方完成の計算では，早さと正確さが重要です
暗算して書く量を減らし，答えに直接たどりつくように練習していきましょう
平方完成の応用 y＝ax2＋bx＋c
ｘ2 の係数が１でない場合，ｘ2 の係数でくくってから平方完成の式変形をしていきます
半分にして２乗を引くのは同じだね♪
ポイントは，ｘ2 の係数でくくること，｛ ｝を掛け算してはずすことだよ！
★補足★ 平方完成が必要ない式と必要な式の区別
「そもそもどんな式で平方完成をする必要があるの？」
この大事な疑問を解消しておきましょう
平方完成が必要か必要でないか判断がつかないと，実際の問題で困ってしまいますからね…
なるほど！ｘがないかあるかで判断すればいいんだね♪
それでは本時のまとめです
- 軸の方程式と頂点の座標が分からない形の場合，平方完成の式変形が必要
- 平方完成の目的は，軸の方程式と頂点の座標を求めること
- 平方完成の方法は２つ。①ｘの係数を半分にする，② ①で半分にした値の２乗を引く
- 慣れてきたら暗算をして途中計算をとばすとよい
- ｘ2 の係数が１でない場合，ｘ2 の係数でくくってから平方完成の式変形
- 平方完成が必要ない式と必要な式の区別は，ｘがないかあるか
平方完成の式変形をする目的は，軸の方程式と頂点の座標を求めることです
２次関数の単元では，何度も使用する必須知識であるため，早く正確になるべく暗算で平方完成ができるように練習しておきましょう
今回は以上です。ありがとうございました
