箱ひげ図って何?

データの散らばりを分析できる図のことだよ!
ということで本時は
- 箱ひげ図(はこひげず)について知りたい
- 箱ひげ図によってデータの散らばりを分析したい
- 四分位数と箱ひげ図の関連を知りたい
こんなあなたに向けた内容です
箱ひげ図はデータの散らばりを視覚的に分析できる優れものです!
箱ひげ図を読み取ることで,何となくではなく根拠を持ってデータを分析できるようにしていきましょう
さっそく本時の結論です
箱ひげ図の5つの指標と2つのポイントで,データの散らばりを分析しよう!

データの散らばり

箱ひげ図とは
箱ひげ図とは,データの散らばりを1つの図で表したものです
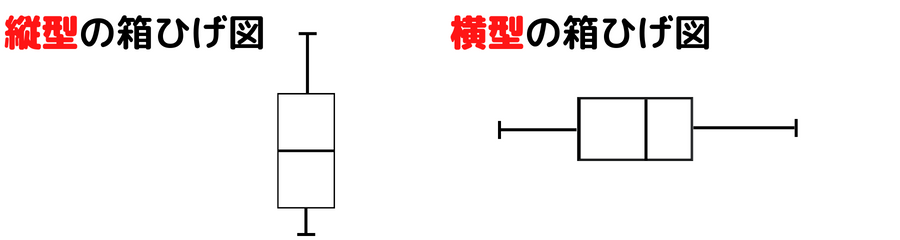

縦型と横型があるよ
箱ひげ図には縦の向き(縦型)と横の向き(横型)があります

なんで❝箱ひげ図❞って言うんだろう?

図をよく見ると❝箱❞と❝ひげ❞に見えるでしょ⁉笑
箱ひげ図の名前の由来は,その言葉通り図の形が❝箱❞と❝ひげ❞に見えるからです
箱ひげ図(はこひげず、箱髭図、英: box plot、box-and-whisker plot)は、データのばらつきをわかりやすく表現するための統計図である。主に多くの水準からなる分布を視覚的に要約し、比較するために用いる。ジョン・テューキーが1970年代に提唱した。様々な分野で利用されるが、特に品質管理で盛んに用いられる。箱(box)と、その両側に出たひげ(whisker)で表現されることからこの名がある
箱ひげ図 – Wikipedia

1970年というと約50年前だから比較的最近だね
【データの分析】の単元は現代社会を生きる上で必須知識です
学習内容もここ何十年かの間に整えられてきているので,数学の歴史と比べたら箱ひげ図の歴史は浅いですね
箱ひげ図の5つの指標
箱ひげ図を書くために必要な5つの指標を小さい順に紹介します
- 最小値
- 第1四分位数Q1(下の組の中央値)
- 第2四分位数Q2(中央値)
- 第3四分位数Q3(上の組の中央値)
- 最大値
5つの指標が箱ひげ図の❝どこ❞を表すのか確認しましょう
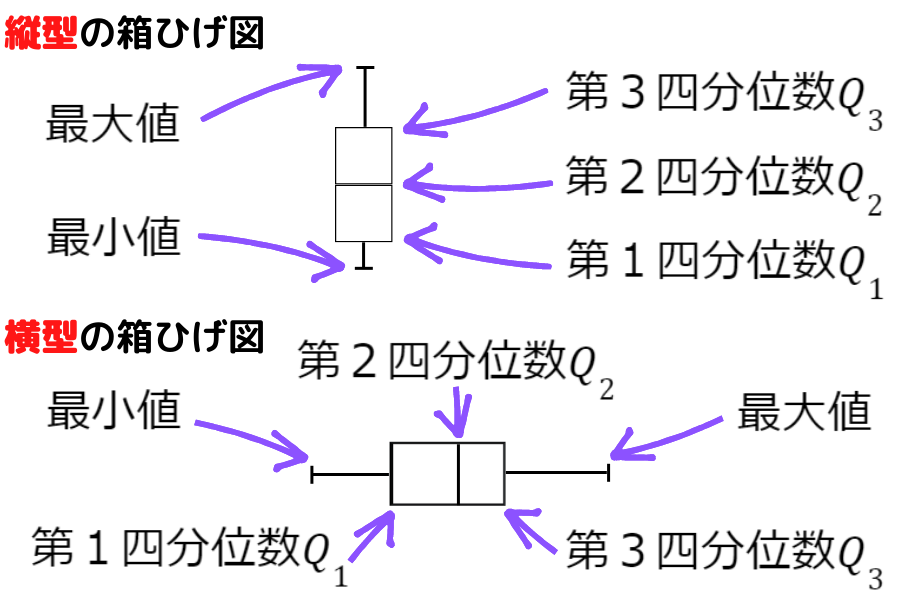

『縦型は下から』『横型は左から』小さい順に並ぶよ
箱ひげ図の5つの指標は,縦型は下から小さい順に,横型は左から小さい順に5つの指標が並びます
第1四分位数Q1・第2四分位数Q2・第3四分位数Q3については,こちらの授業で復習してくださいね
また,データの代表値として学習した平均値・最頻値・中央値ですが,箱ひげ図で使用するのは中央値(=第2四分位数)のみです
とくに❝平均値❞を使用しない点に気をつけましょう
正しく言えば箱ひげ図に平均値を示すこともありますが,数学Ⅰで出題される箱ひげ図に平均値が載ることはありません

箱ひげ図には平均値は必要ないよ
データの代表値(平均値・最頻値・中央値)については,こちらの授業で復習してください
箱ひげ図の5つの指標の読み取り方【テクニックを紹介】
箱ひげ図でデータの散らばりを読み取るのにはコツがあります
下の図で確認してみましょう
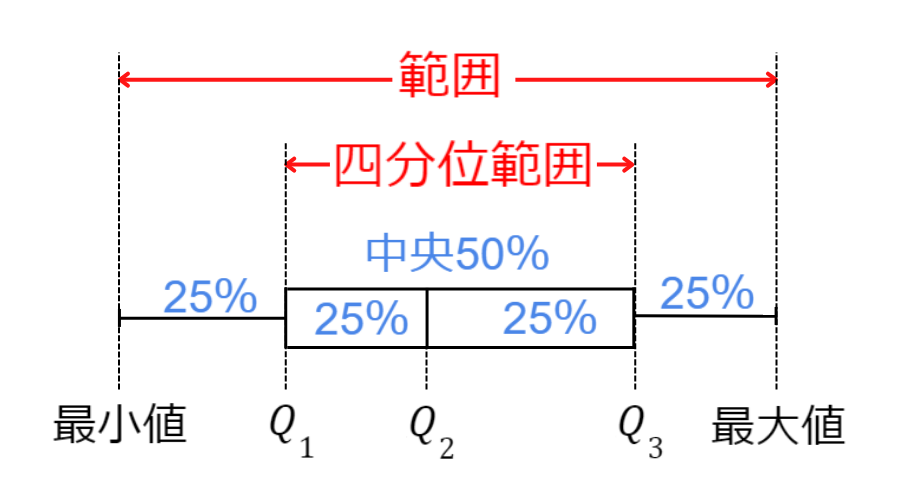
ポイントは2つです
- 範囲と四分位範囲が読み取れる
- ❝箱❞と❝ひげ❞によって25%ずつに区切られる
5つの指標に加えて,上記のポイント2つを頭に入れて問題を考えるのがオススメです!
箱ひげ図によるデータの散らばりの分析【例題】
では実際の箱ひげ図から,データの散らばりの分析をしていきましょう
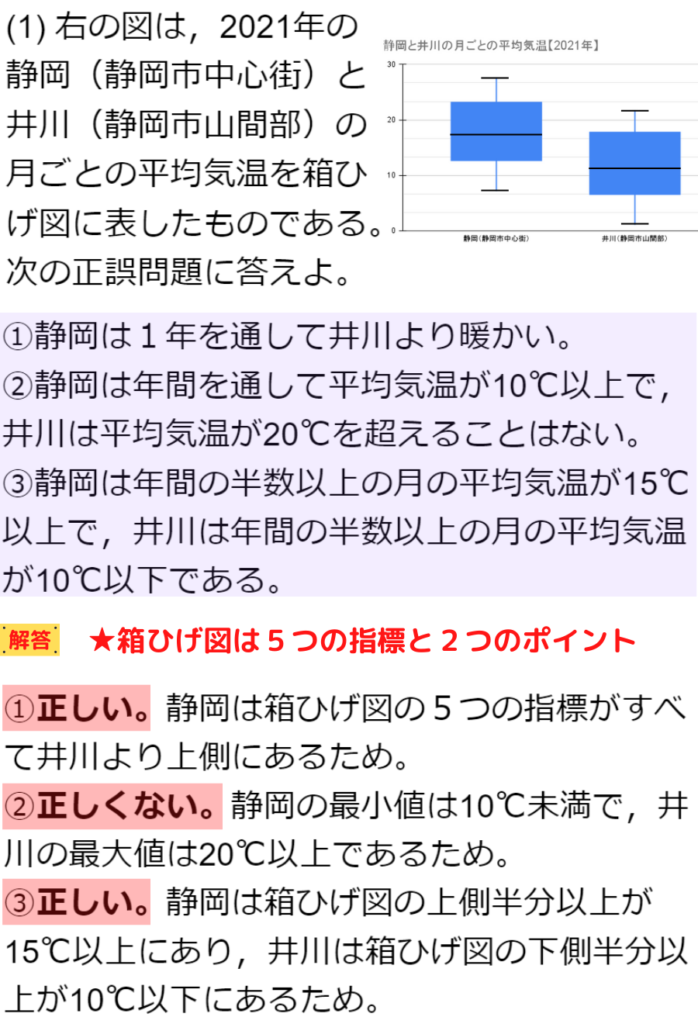

5つの指標と2つのポイントで判断できるよ

たしかに!箱ひげ図って面白いね♬
今回は縦型の箱ひげ図の読み取りをしましたが,もちろん横型でも同じです
箱ひげ図の5つの指標と2つのポイントで正しいか正しくないか判断するようにしてくださいね!
また,複数のデータの分布を比較するときに箱ひげ図は有効であることが分かりますね
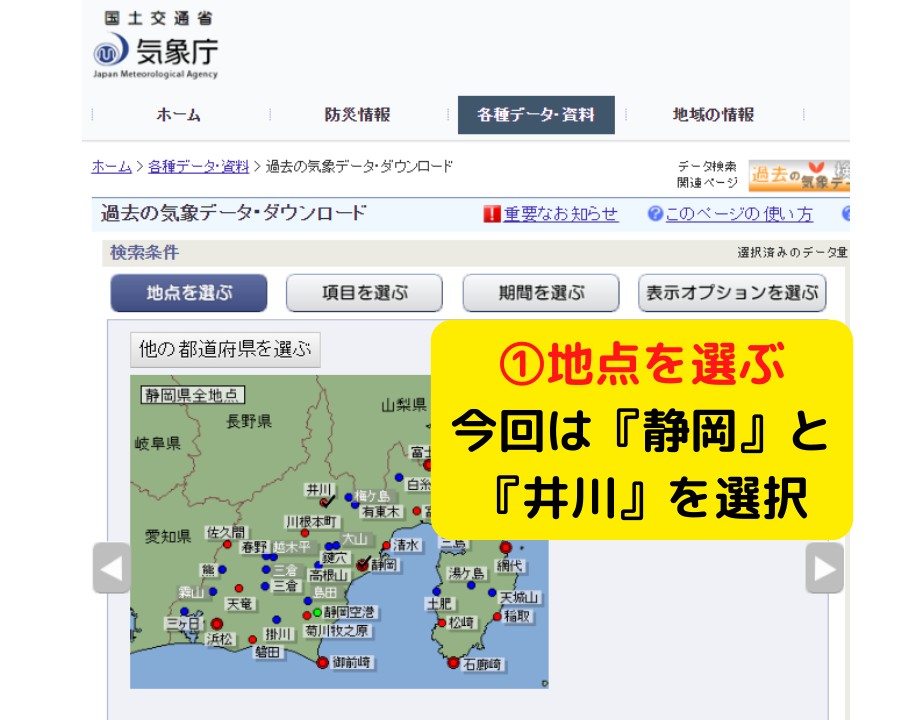
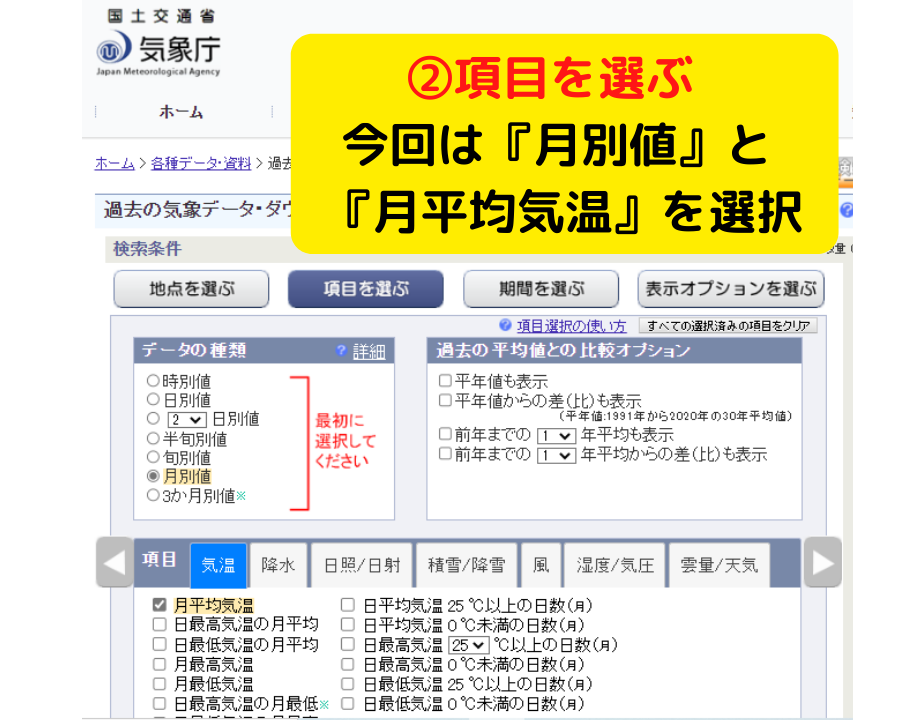
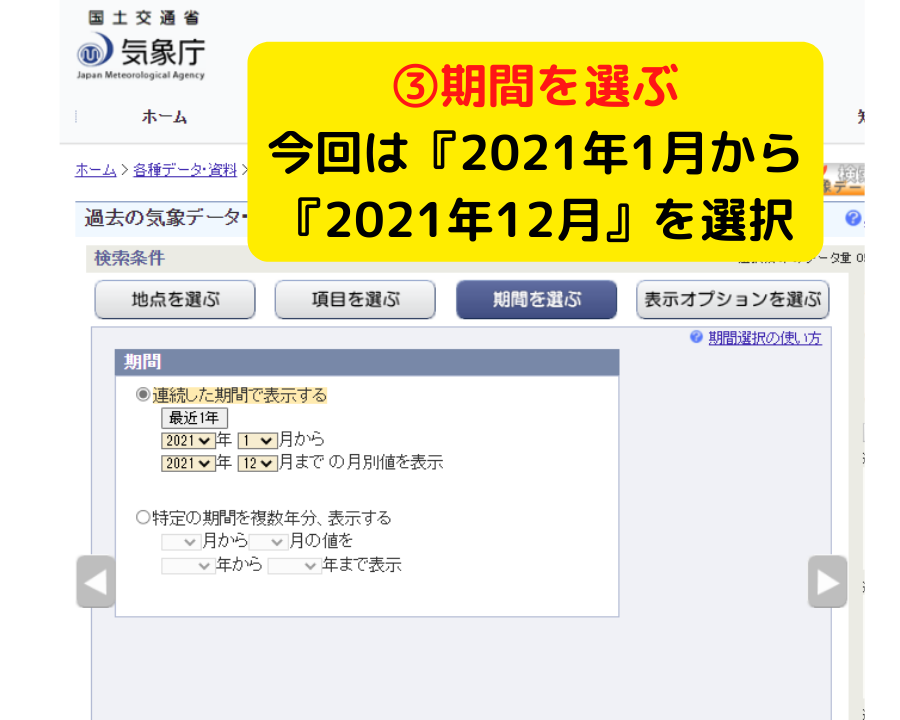
★補足①★ 授業で使える!気象データの取り寄せ方法【気象庁】
今回使用した箱ひげ図の元データは,気象庁のホームページから取得しました
静岡市の静岡と井川の2021年の平均気温に限らず,他県の様々な気象情報を取得可能です!
授業で気象データを使いたい!!
そんなあなたに非常にオススメです♬

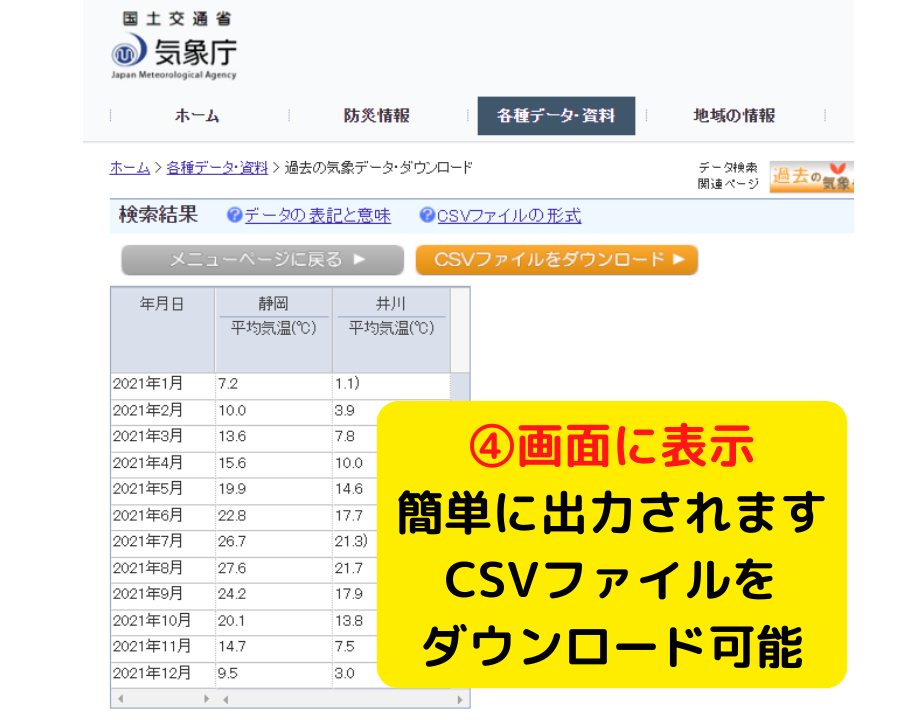
CSVでファイルをダウンロードできるよ
取得したデータはCSVファイルをダウンロードできるので,『エクセル』や『Googleスプレッドシート』で簡単に箱ひげ図を作成可能です!
とっても簡単ですのでぜひ授業で活用してみてくださいね♬
★補足②★ 「数学I」だけでなく「情報I」にもデータの分析を学習する!?
みなさんご存知でしたか?
『データの分析は数学の「数学I」の科目だけでなく,情報の「情報I」でも学習する』のです
データの分析は数学の専売特許ではありません

えっ…「情報I」でもデータの分析を勉強するの⁉️

そう!勉強内容が重なる部分も多いよ
さらに,2025年から国公立大学の受験に必要な科目が,5教科7科目から「情報I」を加えて6教科8科目になります
つまり2022年4月(令和4年度)入学の高校生から「情報I」の重要性が高まっているため,数学における「データの分析」の重要性も高まっているといえるでしょう
データの分析ってそれだけ現代社会に必要な知識であることの裏返しでもありますね!

【まとめ】箱ひげ図でデータの散らばりを素早く分析しよう!
それでは本時のまとめです
- 箱ひげ図には縦型と横型がある
- 図の形が箱とひげに見えることから箱ひげ図と命名された
- 考案されたのが1970年代と箱ひげ図の歴史は浅い
- 箱ひげ図は5つの指標(最小値・第1四分位数Q1・第2四分位数Q2・第3四分位数Q3・最大値)を用いる
- 5つの指標と2つのポイント(①範囲と四分位範囲,②25%ずつに区切られる)で分析するとよい
- 気象庁のホームページから気象データを簡単に取得できる
- 「数学I」だけでなく「情報I」にもデータの分析の学習がある
本時は箱ひげ図について学習しました
実にシンプルな図である箱ひげ図…
シンプルであるからこそ誰もが利用しやすい分析ツールとして活用できると言えますね!
5つの指標と2つのポイントで,データの分析が得意になってくれると嬉しいです
今回は以上です。ありがとうございました
 サッカークロス
サッカークロス