サッカークロス 
こんにちは，madoryです！
座標を用いた三角比の定義から，
0°，90°，180°の三角比の値が計算できたね！
うん！
90°の三角比の値の謎が解けたよ♬
今日は，鈍角（90°＜θ＜180°）の三角比の値を求めていこうね！
例えば『sin 120°』の値が分かるようになるよ‼
直角三角形を用いて定義される三角比は，
座標を用いて定義することで，0°≦θ≦180°まで角度が拡張されました
詳細は過去の授業を参考にしてください
【図形と計量⑤】90°の三角比の謎が解明‼︎座標で考える三角比の拡張
座標を用いて定義したことによって，鈍角（90°＜θ＜180°）の三角比の値が新たに加わります
そこで本時は，
「鈍角（90°＜θ＜180°）の三角比の値を求めましょう！」
さっそく本時の結論です
鈍角の三角比の値は，『120°』『135°』『150°』の３つを理解すればよい！
座標を用いた定義の仕方によって，鈍角の三角比が定義されました
注意点はｘ座標です！！
鈍角の場合，ｘ座標の符号が負（ｘ＜０）になるので気を付けましょう！
実際は180°から θ の角度を引いて，
黄色の直角三角形を考えていくよ！
そもそも鈍角の直角三角形は存在しません
実際に考えていく直角三角形は，『180°ーθ』を計算した黄色の直角三角形になります
実際に具体例を見てみましょう
120°の三角比の値
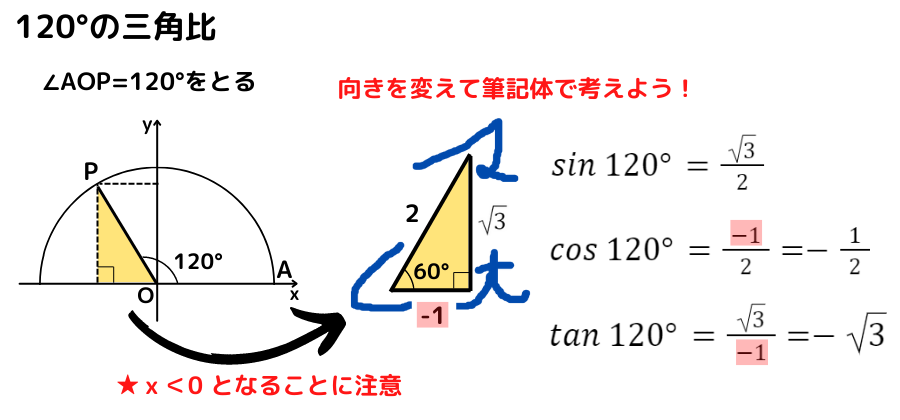
『180°ー120°＝60°』だから，
60°の直角三角形を考えるよ！
なんでｘ座標が負になるの？？
ｘ座標は原点よりも左にくると負の数になるから，
鈍角の場合の直角三角形の横の長さは，常に負になるんだよ‼
120°の三角比の値は，『180°ー120°＝60°』から 60°の直角三角形の三角比の値を考えます
ただ，ｘ座標が負になる点に注意が必要です
135°の三角比の値
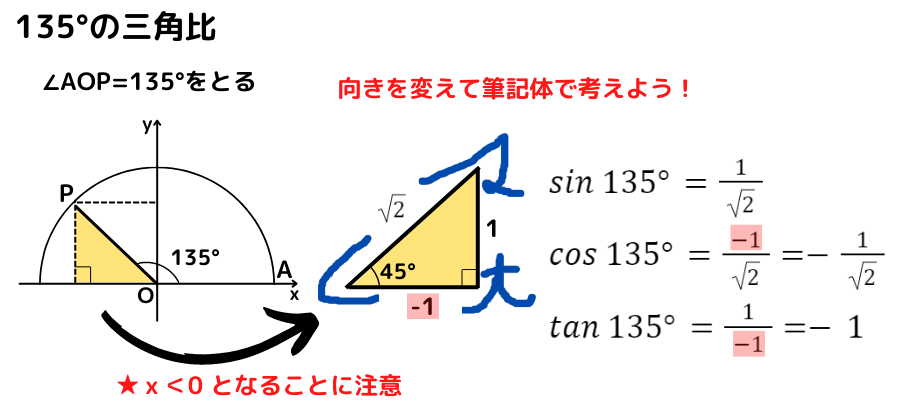
『180°ー135°＝45°』だから，
45°の直角三角形を考えるよ！
135°の三角比の値は，『180°ー135°＝45°』から 45°の直角三角形の三角比の値を考えます
ｘ座標が負になる点に気をつけましょう
150°の三角比の値
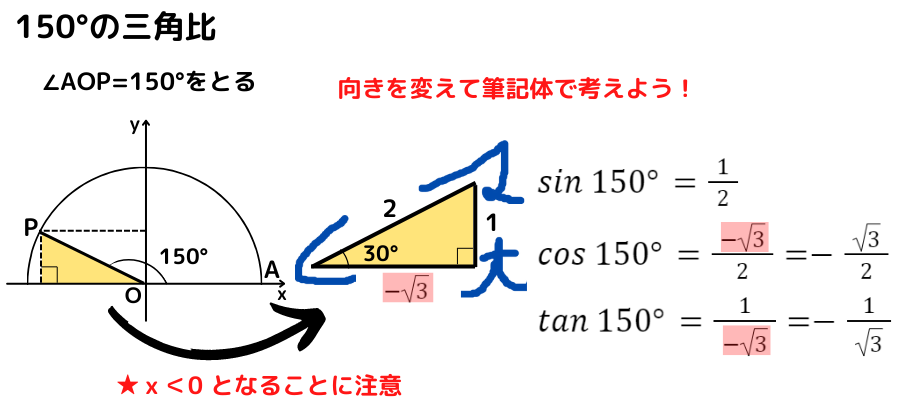
『180°ー150°＝30°』だから，
30°の直角三角形を考えるよ！
150°の三角比の値は，『180°ー150°＝30°』から 30°の直角三角形の三角比の値を考えます
こちらもｘ座標が負になる点に注意が必要です
あれ……。
120°，135°，150°の三角比って，三角定規の直角三角形を考えているね！
その通り！！
30°，45°，60°の三角定規の直角三角形って本当に重要なんだよ♬
逆に，鈍角の三角比の値は，
三角定規の形になる「120，135°，150°」の３つだけ覚えればいいよ！
さて，ここまでを整理しておきましょう
- 120°の三角比の値は，『180°ー120°＝60°』から 60°の直角三角形を考えればよい
- 135°の三角比の値は，『180°ー135°＝45°』から 45°の直角三角形を考えればよい
- 150°の三角比の値は，『180°ー150°＝30°』から 30°の直角三角形を考えればよい
ただし，いずれの場合もｘ座標が負になる点に注意しましょう
ｘ座標が負になると，『cos』と『tan』の値が負になります
鈍角の三角比の値は，「120°，135°，150°」の３つを必ず覚えるようにしましょう
★補足★ 『120°』『135°』『150°』以外の鈍角の三角比の値はどうなるの？
じゃあさ，三角定規の形にならない鈍角の三角比の値ってどうなるの？？
良い質問だね♬
一緒に考えてみよう！！
ここで，120°，135°，150°以外の鈍角の三角比の値を考えてみましょう
例えば，143°の三角比の値はどうなると思いますか？
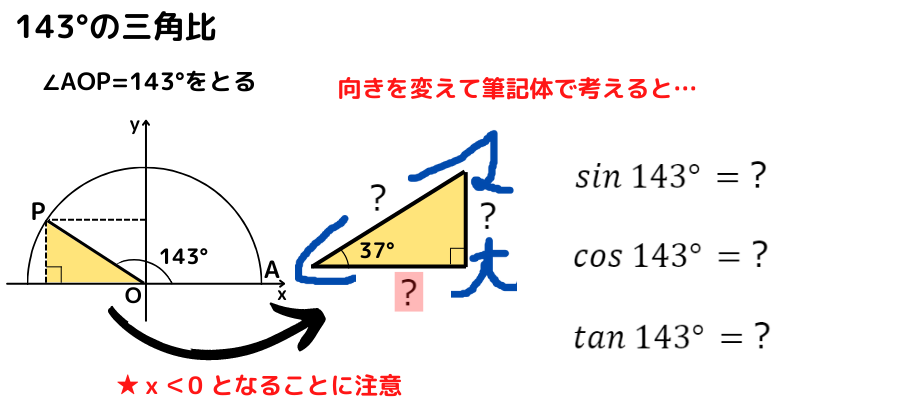
『180°ー143°＝37°』だから，
37°の直角三角形を考えるよ！
37°の直角三角形の辺の長さの比は分からないから，
143°の三角比の値は求められないのかな…
レッサーくん，ちょっと待って！！
0°～90°までの三角比の値が分かる『三角比の表』があったよね！
0°～90°までの三角比の値は常に一定であることから，『三角比の表』の値を利用することができました
詳細は過去の授業を参考にしてください
【図形と計量③】三角比の最強ツール！『三角比の表』
そうだったね！『三角比の表』で値を求めてみよう‼
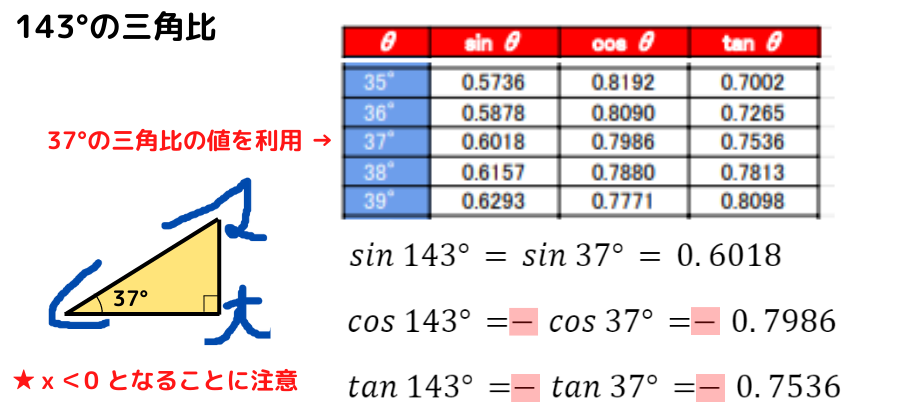
すごい！！『三角比の表』を使って値が求められたね！
『三角比の表』は本当に便利な表なんだ♬
これで鈍角の三角比の値を求められるね！
このように『三角比の表』を用いれば，143°の三角比の値に限らず，すべての鈍角の三角比の値を求めることができます
『三角比の表』って，本当に便利ですよね！
それでは本時のまとめです
- 鈍角の三角比の値は，180°ーθ を考え，ｘ座標が負になる点に注意
- 120°の三角比の値は，『180°ー120°＝60°』から，60°の三角比の値を考えればよい
- 135°の三角比の値は，『180°ー135°＝45°』から，45°の三角比の値を考えればよい
- 150°の三角比の値は，『180°ー150°＝30°』から，30°の三角比の値を考えればよい
- 鈍角の三角比の値は，「120°，135°，150°」の３つを覚えればよい
- 120°，135°，150°の三角比の値は，結局三角定規の直角三角形を考えている
- 120°，135°，150°以外の鈍角の三角比の値は，『三角比の表』を用いてすべて求めることができる
本時は鈍角の三角比の値について学習してきました
特に，120°，135°，150°の三角比の値は，三角定規の形である60°，45°，30°の直角三角形から求めることができました
そして，それ以外の鈍角の三角比の値は『三角比の表』を用いて計算することができました
実際の問題では，『三角比の表』を使用するケースは多くないため，鈍角の三角比の値の基本は「120°，135°，150°」の３つをしっかり覚えてくださいね！
今回は以上です。ありがとうございました
