サッカークロス 
madoryの『高校数学のブログ授業』です
- 数学を基礎から学び直したい高校生
- 高校入学前に予習して備えたい中学生
- 挫折した高校数学に再挑戦したい社会人
こんな❝あなた❞に向けて発信しています！
さっそく本時の結論です
「平方完成するか判断して軸と頂点を求め，頂点の座標からグラフを書く！」
平方完成をすることで，２次関数のグラフの軸の方程式と頂点の座標を求めることができました
平方完成の方法については，こちらの授業を参考にしてください
【２次関数④】平方完成で求める『軸と頂点』
そして，平方完成ができれば，軸の方程式と頂点の座標を求めることができました
軸の方程式と頂点の座標の求め方については，以下の授業を参考にしてください
【２次関数②】グラフ４種類の軸と頂点の求め方
さらに，軸の方程式と頂点の座標を求めることができれば，グラフの書き方は❝５STEP❞で書くことができました
グラフの書き方❝５STEP❞については，次の授業を参考にしてください
【２次関数③】グラフを正確に書く❝５STEP❞
本時では，これまで学習してきた方法を組み合わせて，２次関数のグラフの総仕上げを行っていきます！
２次関数のグラフの書き方❝フローチャート❞
２次関数のグラフを書く際の指針となる❝フローチャート❞がこちらです
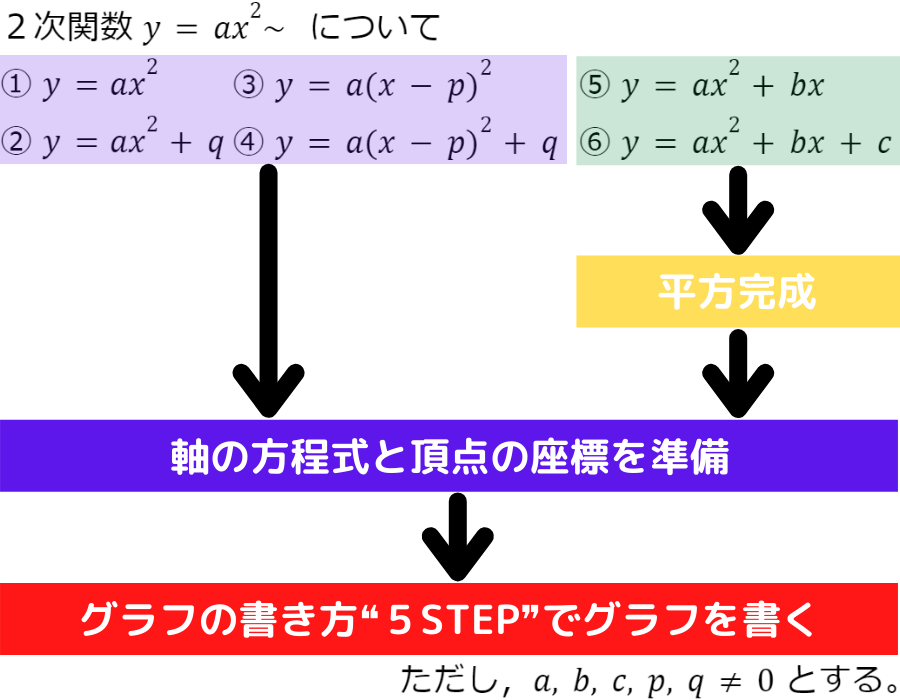
まず，平方完成が必要か判断するんだね！
基本の平方完成 と 応用の平方完成
平方完成の方法については，基本と応用の２種類に分けることができました
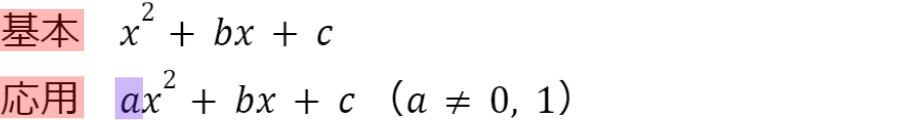
応用の式は，a に１以外の数字が書いてある場合だね！
平方完成が必要な２次関数のグラフ ①基本の平方完成
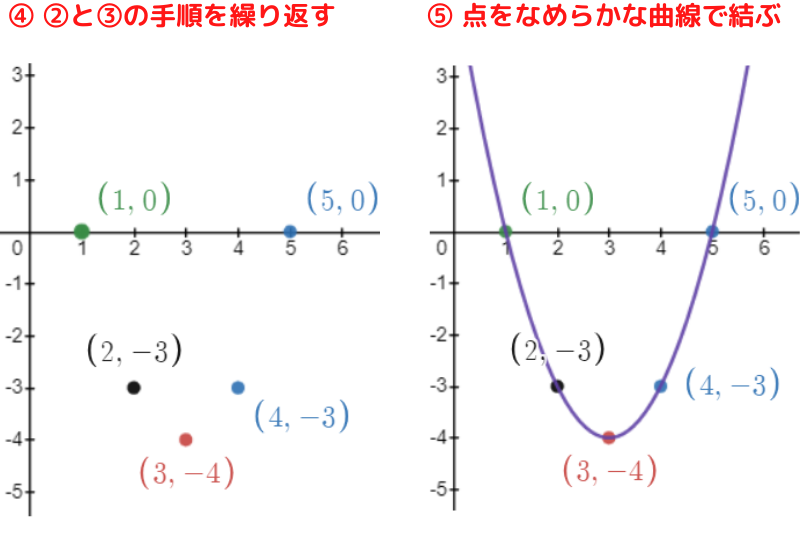
基本の平方完成が必要な２次関数について，グラフの書き方を順番に見ていきましょう
まず平方完成して，
軸の方程式と頂点の座標を準備するよ！
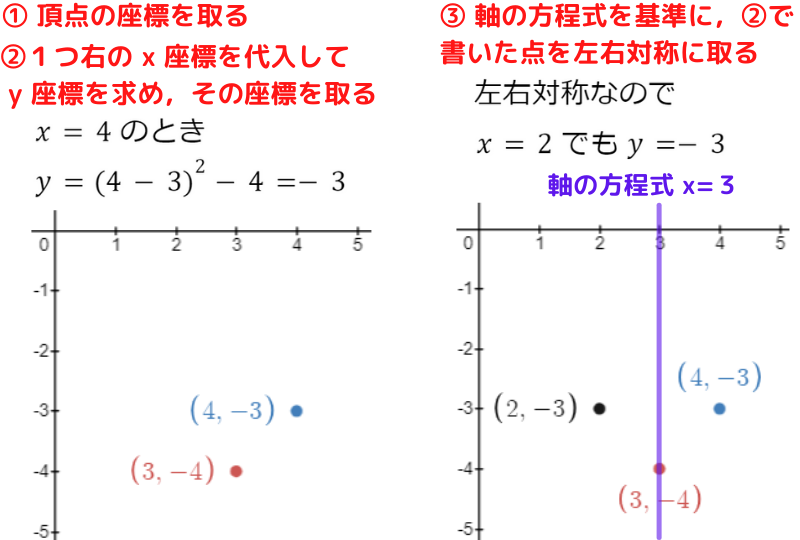
グラフは頂点の座標から書くんだったね！
平方完成が必要な２次関数のグラフ ②応用の平方完成
応用の平方完成が必要な２次関数について，グラフの書き方を順番に見ていきましょう
平方完成してグラフを書く準備はOK!!
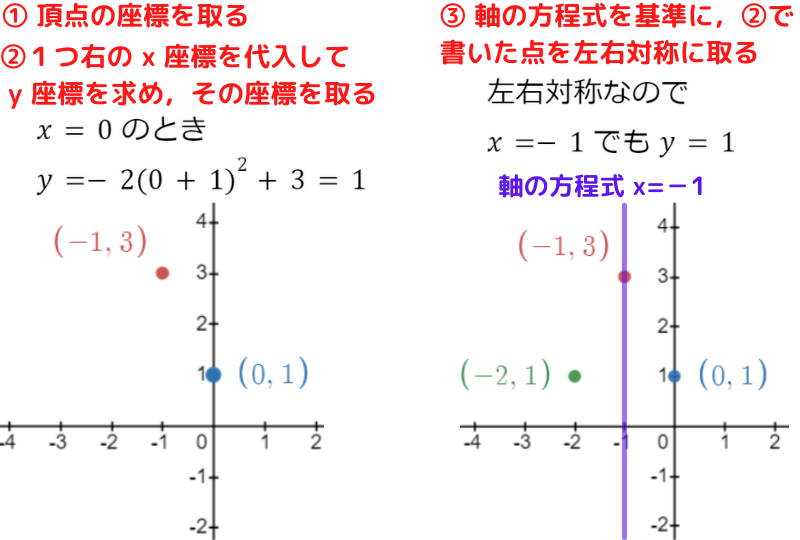
ｘの値を代入してｙの値を求めるときに，
計算ミスしないように注意だね！
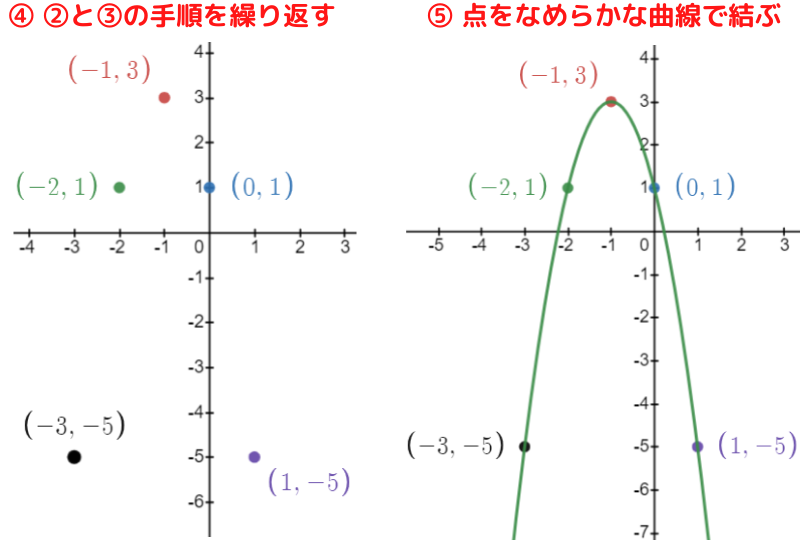
★補足★ ２次関数のグラフの書き方 ❝フローチャート❞具体例
具体例でもフローチャートを確認しておきましょう！
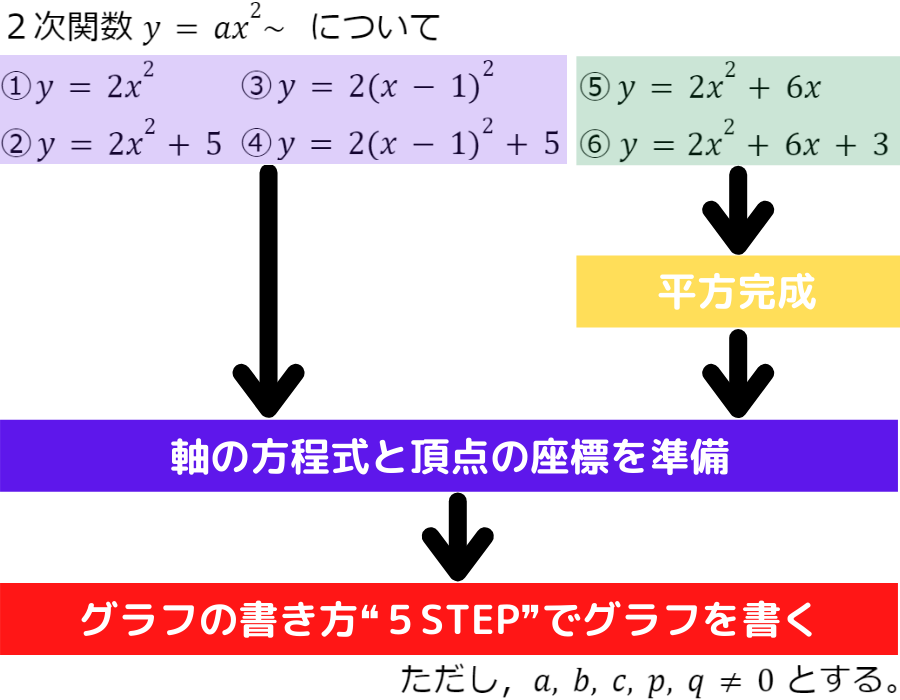
即座に，平方完成が必要かどうか判断できるようにしたいですね！
それでは本時のまとめです
- 平方完成は基本と応用の２種類あり，応用は a が１以外の場合
- グラフを書く際，平方完成が必要であれば，平方完成してから軸の方程式と頂点の座標を準備
- グラフを書く際，平方完成が必要なければ，すぐに軸の方程式と頂点の座標を準備
- 軸の方程式と頂点の座標を準備したら，グラフの書き方❝５STEP❞で書く
- ２次関数のグラフの書き方❝フローチャート❞でパターン化できる
これまでの２次関数の知識を組み合わせることで，どんな式の形でも２次関数のグラフを書くことができるようになりました
平方完成が必要なのかどうか…ここさえ整理できれば難しいことはありません
ぜひフローチャートを活用してくださいね♪
今回は以上です。ありがとうございました
