【２次関数②】グラフ４種類の軸と頂点の求め方

madoryの『高校数学のブログ授業』です

こんな❝あなた❞に向けて発信しています！

【結論】軸と頂点の x 座標は符号逆！下に凸or上に凸は x² の係数が 正or負

さっそく本時の結論です

「軸と頂点の x 座標は符号逆！下に凸or上に凸は x² の係数が 正or負」

１次関数のグラフは直線，２次関数のグラフは曲線となりました

２次関数のグラフは物を投げる（=放る ※ほうる）軌道になるので，放物線（ほうぶつせん）とも呼ばれます

そんな２次関数のグラフを書く上での基礎となる，軸と頂点，下に凸 or 上に凸の考え方を紹介します

ではさっそく結論にしたがって，順番に見ていきましょう

グラフの軸と頂点

まず，２次関数のグラフは左右対称になります

グラフを書く上で大事な情報を確認していきましょう

下に凸 or 上に凸

レッサーくん

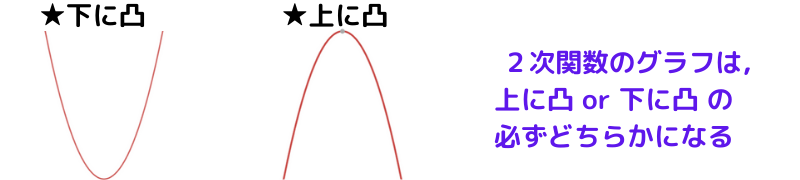
下に凸は振り子の軌道みたいで，上に凸はボールの軌道みたいに，ぼくは見えるな～♪

グラフが下に凸 or 上に凸かは，x² の係数が 正 or 負 かで判断ができます

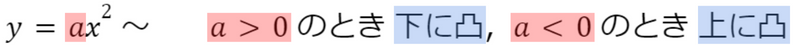
軸と頂点とは？

ホッくん

軸は直線を表し，頂点は点（座標）を表すよ！

軸と頂点の求め方 その１

２次関数のグラフは全部で４種類に分けられます

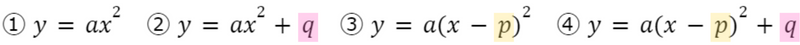
それぞれの軸の方程式と頂点の座標について整理します

ホッくん

軸と頂点の x 座標は符号が逆になるよ！

軸と頂点の求め方 その２

次に，具体例で軸と頂点の求め方を確認しましょう

レッサーくん

x² の係数は下に凸or上に凸を表しているけど，

軸と頂点には関係がないんだね！

ホッくん

軸と頂点の x 座標は符号が逆になっているね！

かっこ(　)² の中の数から，軸と頂点の x 座標を求めますが，符号が逆になります

軸の方程式・頂点の x 座標の符号を間違えないように注意が必要ですね！

★補足★　象限

x 軸と y 軸の座標平面を考える際には，象限（しょうげん）の知識が必須です

ホッくん

各象限で，x 座標と y 座標の符号が変わることになるね！

【まとめ】４種類ある２次関数のグラフの，軸と頂点を整理して覚えよう！

それでは本時のまとめです

いかがだったでしょうか？

まとめを見た際に，本時の内容が頭に思い浮かんでもらえたら嬉しいです

今回は以上です。ありがとうございました