サッカークロス 
こんにちは，madoryです！
本時は座標を用いた三角比の定義について学習していきます
レッサーくん！
三角比の角度 θ って最大何度までだと思う？
三角比って直角三角形を考えてきたよね！
三角形の内角の和が180°だから…
分かった！最大90°だね！！
その通り！厳密に言えば90°未満になるね‼
そういえば三角比の表を学習したけれど，90°の値も表に書いてあったよ！！
一体どういうことなんだろう…？？
以前，三角比の表について学習してきました
0°～90°までの三角比の値が一覧にまとめられた表でしたね！
詳細は過去の授業を参考にしてください
【図形と計量③】三角比の最強ツール！『三角比の表』
三角比の表には，0°も90°も記載されていました
角度 θ は直角三角形の１つの角度なので，0°と90°はおかしいですよね！？
レッサーくん，今日は90°の三角比も考えることができる
座標を用いた三角比の定義について勉強していくよ♬
三角比の表に書かれた90°の値の謎が分かるんだね‼
楽しみ～♬
本時で学習する座標を用いた三角比の定義を学習すると，
「三角比の表に書かれている，0°や90°の三角比の謎が解明します！」
さっそく本時の結論です
座標を用いて三角比を定義すると 0°～180° まで角度が拡張され，0°，90°，180°の三角比の値が計算できる！
直角三角形を用いた三角比の定義（これまで）
三角比の定義は次のように学習しました
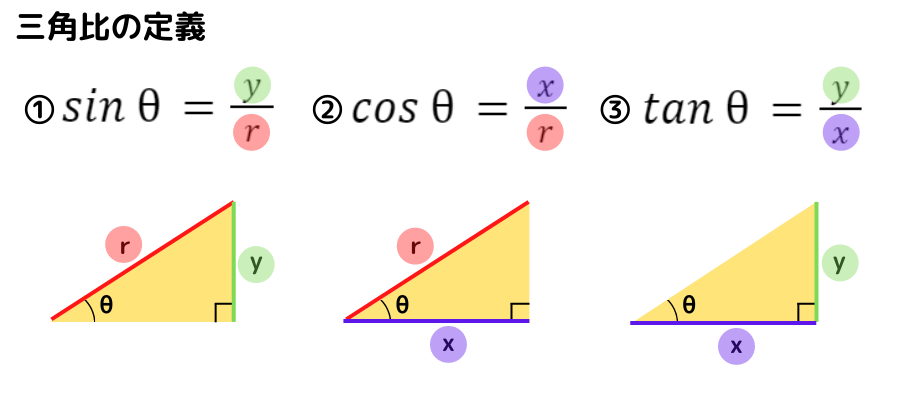
詳細は過去の授業を参考にしてください
【図形と計量①】あなたはどれ派？三角比の定義の暗記方法３選
直角三角形の２辺を用いて三角比を定義しましたね
ということは，θ の大きさは『 0°＜ θ ＜ 90° 』になりますね！
この定義の仕方では，三角比の表に 0° や 90° の値が書かれているのはおかしいことになります
座標を用いた三角比の定義（これから）
座標平面上における新しい三角比の定義の仕方について紹介していきましょう
- まず，原点 О を中心とする半径ｒの半円を書く
- 半円とｘ軸の正の部分との交点Ａ，半円上の点Ｐ，原点Ｏとのなす角を θ とする
- ∠ＡＯＰ＝ θ とし，線分ＯＰを斜辺とする直角三角形において，三角比を定義する
言葉では分かりづらいですね…図で見てみましょう！
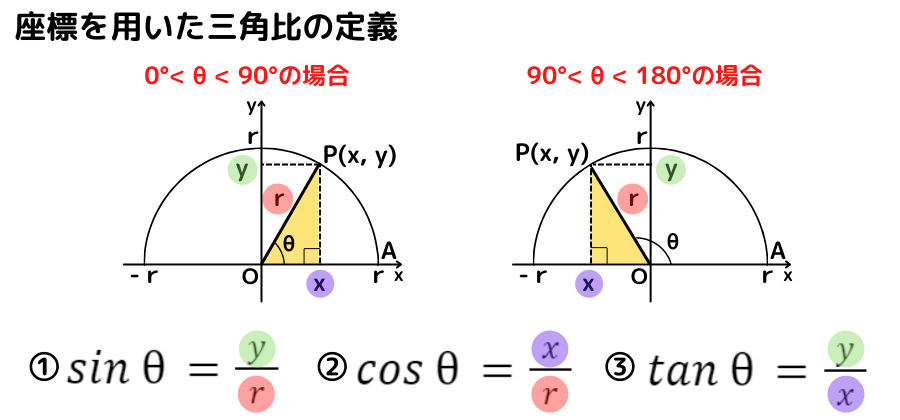
座標を用いて定義すると，
90°より大きい鈍角の直角三角形の三角比が求められるよ♬
0°＜θ＜90° のときは，これまで通りの直角三角形を用いた定義と同じように考えることができます
また，90°＜θ＜180° のときが新たに定義され，例えば『sin120°』のように，鈍角の直角三角形について考えることができるようになります
あれ…，
0° や 90° の三角比の値はどうなるの？
よく気付いたね！
0°，90°，180°の三角比も座標を用いると定義できるんだ♬
座標を用いて定義すると，0°＜θ＜90°，90°＜θ＜180° に加え，0°，90°，180°の三角比の値も決まります
ただ，ちょうどｘ軸上もしくはｙ軸上に点Ｐがくるため，直角三角形を作って考えることはできません
0°，90°，180°の三角比の値がどうなるのか，具体的に確認していきましょう
0° の三角比
『ｘ座標にｒ，ｙ座標に０』を三角比の定義に代入すると求まるよ！
90° の三角比
『ｘ座標に０，ｙ座標にｒ』を三角比の定義に代入すると求まるよ！
あっ！！90°の三角比の値が求まったね！
この値が三角比の表に書いてあったんだね‼
そうなんだ！
座標を用いて定義することで，90°の三角比の値が決まるんだ♬
180° の三角比
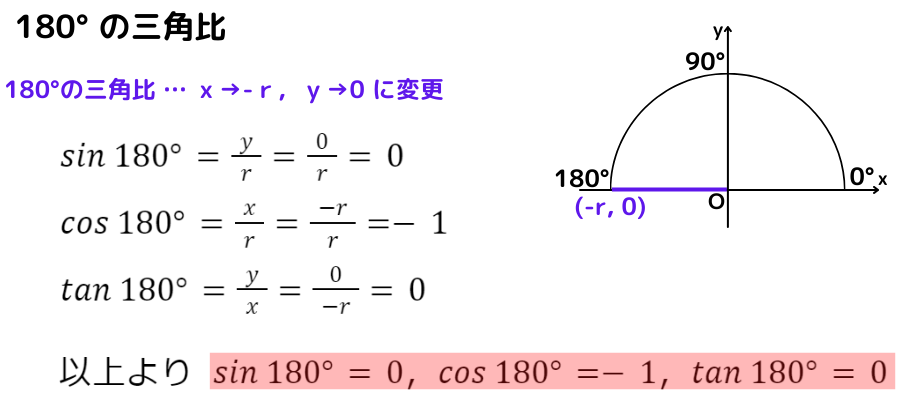
『ｘ座標にーｒ，ｙ座標に０』を三角比の定義に代入すると求まるよ！
0°，90°，180°の三角比のまとめ
それではここで，0°，90°，180°の３種類の三角比の値をまとめましょう
これらの値はすぐに答えられるようにしておこうね！
0°，90°，180°の三角比の値は，ｘ座標とｙ座標の変化によって計算することができました
値としては簡単なものなので，暗記して覚えてしまってもいいですね！
★補足★ なぜ半円で定義するのか？
ねえ，ホッくん！
なんで座標を用いて定義するとき❝半円❞なの？
普通の❝円❞だとダメなのかな？？
良い点に気づいたね！！
なるべく難しくならないようにこの単元では❝半円❞で学習するんだ～。
ということは…
本当は❝円❞で考えることもできるの？？
その通り！！
この分野の続きの学習をする『数学Ⅱ』の『三角関数』という単元では，
❝半円❞でなく❝円❞で考えることになるんだよ‼
みなさんも，
「なぜ，座標を用いて定義するときに❝半円❞で考えるの？？」
こんな疑問が浮かびませんでしたか？
普通の１周分の❝円❞でなく❝半円❞であるのはなぜなのか…
それはただ単に，❝円❞の方が難しくなるから❝半円❞にしているのです
半円だと「0°≦θ≦180°」ですが，円だと「0°≦θ≦360°」まで広がりますよね？！
計算が大変になるので，『数学Ⅰ』の『図形と計量』の単元では❝半円❞で考えることにして，今後学習していく『数学Ⅱ』の『三角関数』という続きの単元では❝円❞で考えていくのです
それでは本時のまとめです
- 直角三角形を用いた三角比の定義は，0°＜θ＜90°
- 座標を用いて三角比を定義すると，0°≦θ≦180°。
- 0°＜θ＜180°までは直角三角形ができるが，0°，90°，180°は直角三角形ができない
- 0°，90°，180°の三角比の値は，ｘ座標とｙ座標の変化に注目して計算ができる
- ❝円❞だと難しくなるから『数学Ⅰ』の『図形と計量』の単元では❝半円❞で学習する
本時は三角比の拡張について学習をしてきました
これにより，0°＜θ＜90°に加え，90°＜θ＜180°の直角三角形を考えることができるようになりました
さらに，ｘ座標とｙ座標の変化に注目すれば，0°，90°，180°の三角比の値も計算ができるため，0°≦θ≦180°までの三角比の値を定義することができるようになりました
0°，90°，180°の三角比の値はすぐに答えられるようにしてくださいね！
今回は以上です。ありがとうございました
