サッカークロス 
こんにちは，madoryです！
レッサーくん！
三角形の面積の求め方っていくつ知ってる？？
中学校で勉強した『底辺 × 高さ ÷ 2 』と
２辺とその間の角を使う『三角形の面積の公式』の２つ知ってるよ♬
今日はさらに三角形の面積の求め方の公式を新たに２つ紹介するよ！
中学校で勉強した『底辺 × 高さ ÷ 2 』
この求め方と三角比の考え方を組み合わせて，前回の授業では２辺とその間の角を用いた『三角形の面積の公式』を紹介しました
詳しくはこちらの記事を参考にしてください
【図形と計量⑩】三角形の面積の求め方『２辺とその間の角』『３辺』
本時はそれに加えてさらに，
「三角形の面積の求め方の公式を新たに２つ紹介します！」
さっそく本時の結論です
『内接円の半径』と『ヘロンの公式』で，三角形の面積公式は４つに増える！
公式
まず，三角形の３辺に接する円を内接円といいます
内接円の半径をｒとすると，次の公式が成り立ちます
三角形の内接円の半径と３辺から成り立つ公式だよ！
この『内接円の半径』を用いた三角形の面積の公式は，内接円の半径と３辺を代入することで面積が求まります
しかし実際には，３辺と面積を代入して内接円の半径を求めるケースが多いです
公式の証明
どのように『内接円の半径』を用いた三角形の面積の公式が成り立つのか…証明を確認していきましょう
３つの三角形の面積の和から△ABC の面積を計算しているよ！
『内接円の半径』を用いた三角形の面積の公式は，上記のように簡単に証明可能です
公式を忘れてしまった場合に備え，自力で公式を作れるように理解しておきましょう！
公式を用いた問題
あれ…以前勉強したことがあるような…
３辺の長さから面積を求める部分は『三角形の面積の公式』の授業で学習したよ！
今回はそこからさらに進んで，内接円の半径を求めているんだ♫
実はこの問題…『三角形の面積の公式』の授業で学習した問題と同じです！
３辺の長さから三角形の面積を求めた後に，内接円の半径を求める部分が追加されています
『内接円の半径』の面積の公式は，３辺と面積を代入して内接円の半径を求める場合に用いる場合が多いです
公式
小文字の ❝s❞ と大文字の ❝S❞ の違いに注意が必要だよ！
ヘロンの公式は三角形の３辺の長さのみから，面積を求めることのできる公式です
公式を使用する際の注意点は，小文字の❝ｓ❞と大文字の❝Ｓ❞の違いです
まず３辺の長さから小文字の❝ｓ❞を求めて，この値と３辺の長さを面積❝Ｓ❞の式に代入していくのです
公式の証明
どのように『ヘロンの公式』が成り立つのか…証明を見ていきましょう
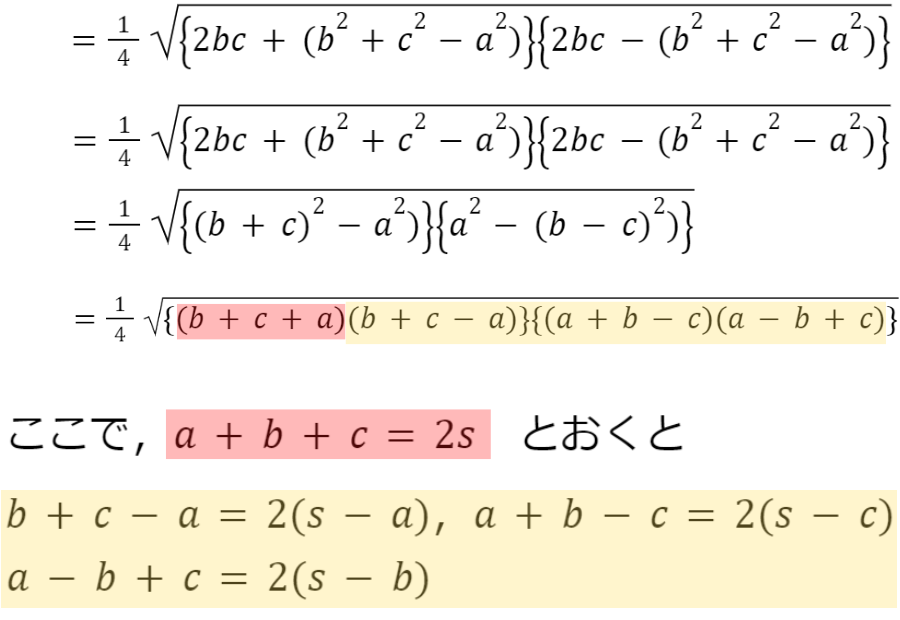
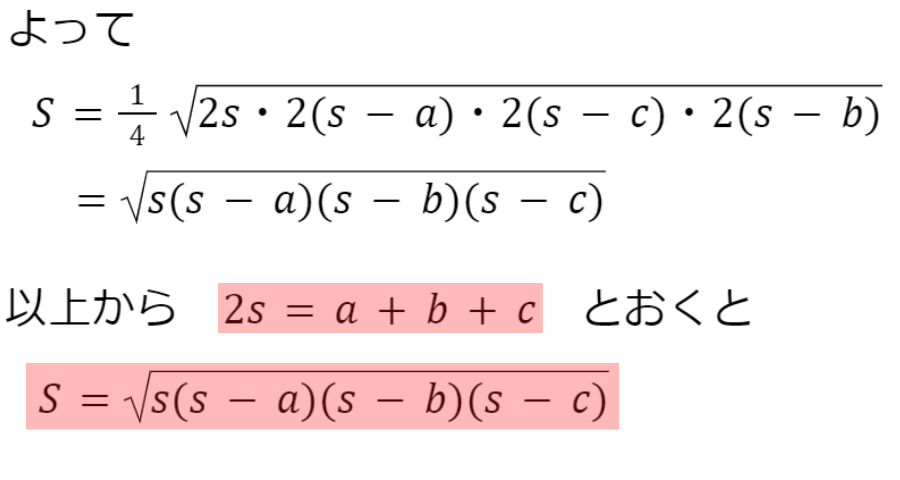
なんとも複雑な計算だ……
もちろん全部覚えておく必要はないよ！
流れを理解しておくだけでも『2s＝a+b+c』が頭に入りやすくなると思うよ♫
公式を用いた問題
ヘロンの公式を使うと，3辺の長さから簡単に三角形の面積が求めるね！
問題に与えられた3辺の長さによっては計算に苦労することも多いんだ…
あくまでも″知っておくと良い″程度の位置付けの公式なんだよ！
今回の問題は，ヘロンの公式を用いて簡単に三角形の面積を求めることができました
しかし，ルートの計算を含む性質上，３辺の長さによっては複雑な計算になることも多いです
そのため，ヘロンの公式はあくまでも補足として理解をしておくのがオススメです
★補足★ なぜ″ヘロン″の公式と呼ぶのか？？
なんで『ヘロンの公式』って呼ぶの？
ヘロンってどういう意味なのかな？？
数学には公式の発見者の名前をつけることがあるんだよ！
ヘロンの公式はヘロンさんが発見したんだ♫
『ヘロンの公式』…なんだかカッコ良いネーミングですよね！
数学の公式名にもその発見者の名前が使用されることがあります
そうです！！『ヘロンの公式』はヘロンさんが発見したのです！
・古代ローマのアレクサンドリアで活躍したギリシャ人の工学者・数学者
・蒸気の圧力を利用した様々な仕掛けを考案した
・主な発明に，蒸気タービンや蒸気を使った自動で開く扉などがある
・数学では測量法の改良者として知られる
・彼の著書「Metrica」の中で証明を示したことから名前を付けられた
（参考；https://ja.wikipedia.org/wiki/アレクサンドリアのヘロン）
公式の名前になっているだけあって結構すごい人なんだね…！
それでは本時のまとめです
- 『内接円の半径』の面積の公式の証明は簡単であるため，公式を忘れた場合に備えて公式の作り方を覚えておくと良い
- 『内接円の半径』の面積の公式は，三角形の３辺と面積から内接円の半径を求める場合に用いることが多い
- 『ヘロンの公式』は小文字の“s“と大文字の“S“の違いに注意
- 『ヘロンの公式』は３辺の長さから三角形の面積を計算できるが，問題によっては計算が複雑になることも多い
- 『ヘロンの公式』は古代ローマの数学者ヘロンから命名された
本時は三角形の面積の公式を新たに２つ紹介しました
これによって，三角形の面積の公式は４つあることになりますね！
最後に整理しておきましょう！
①『底辺 × 高さ ÷ 2 』・・・中学校で学習済み
②『三角形の面積の公式』・ ・・２辺とその間の角（sin）が必要
③『内接円の半径』・・・３辺と内接円の半径が必要だが，３辺と面積から内接円の半径を求めることが多い
④『ヘロンの公式』・・・３辺が必要だが，計算が複雑になる場合もある
高校数学で最もよく使用するのは②です
②を基本としながら，①③④も問題によって使えるようにしたいですね♫
今回は以上です。ありがとうございました
