サッカークロス 
madoryの『高校数学のブログ授業』です
- 数学を基礎から学び直したい高校生
- 高校入学前に予習して備えたい中学生
- 挫折した高校数学に再挑戦したい社会人
こんな❝あなた❞に向けて発信しています！
さっそく本時の結論です
「まず頂点の座標を基準に取り，軸の方程式を基準に左右対称に点を取る！」
この結論にしたがって，順番に見ていきましょう
２次関数のグラフを書くためには，軸と頂点が必須です
軸と頂点の求め方の詳細は，過去の授業を参考にしてください
【２次関数②】グラフ４種類の軸と頂点の求め方
２次関数のグラフを正確に書く手順❝５STEP❞
２次関数のグラフを正確に書くための手順は以下の通りです
- 頂点の座標を取る（点を打つ）
- １つ右の x 座標を代入して y 座標を求め，その座標を取る
- 軸の方程式を基準に，②で書いた点を左右対称に取る
- ②と③の手順を繰り返す
- 点をなめらかな曲線で結ぶ
２次関数のグラフは全部で４種類ありました
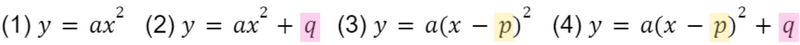
(1) から順番に，具体例でグラフの書き方を見ていきましょう
(1) y＝2x2 軸の方程式 x＝0，頂点の座標 (0, 0)
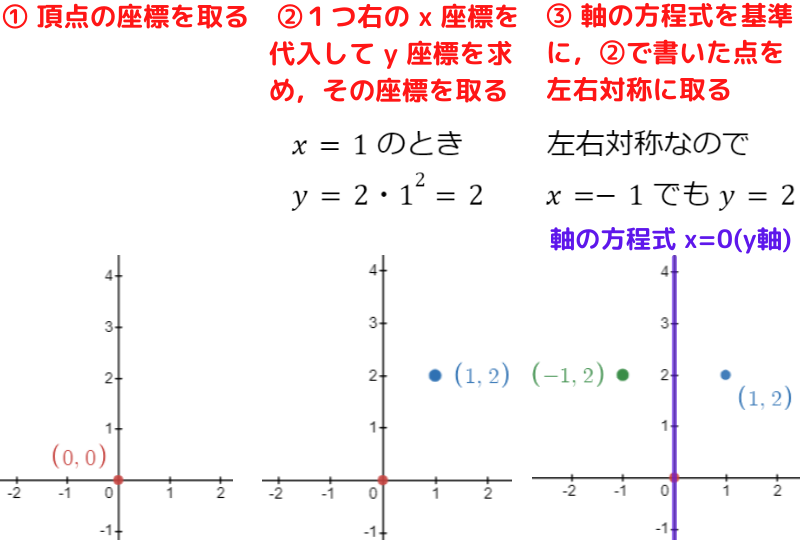
軸の方程式が x=0 (y軸) だから，
y軸を基準にして左右対称に点を取ればいいよ！
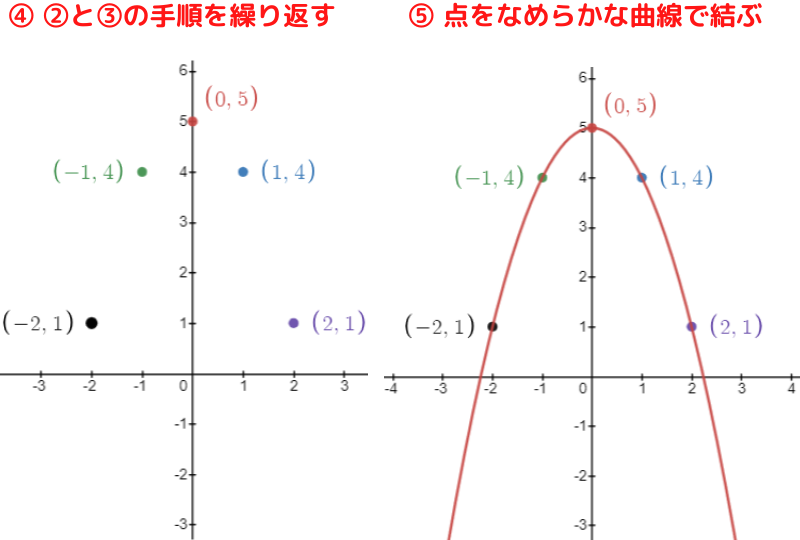
２次関数のグラフはなめらかな放物線だから，
点と点を直線でまっすぐ結んではいけないんだね！
(2) y＝－x2＋5 軸の方程式 x＝0，頂点の座標 (0, 5)
軸の方程式が x=0 (y軸) だから，
y軸を基準にして左右対称に点を取ればいいよ！
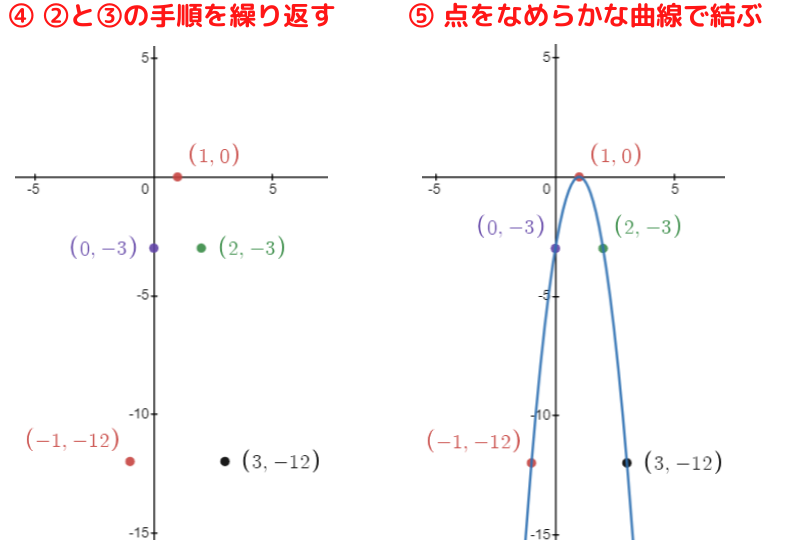
(3) y＝－3(x－1)2 軸の方程式 x＝1，頂点の座標 (1, 0)
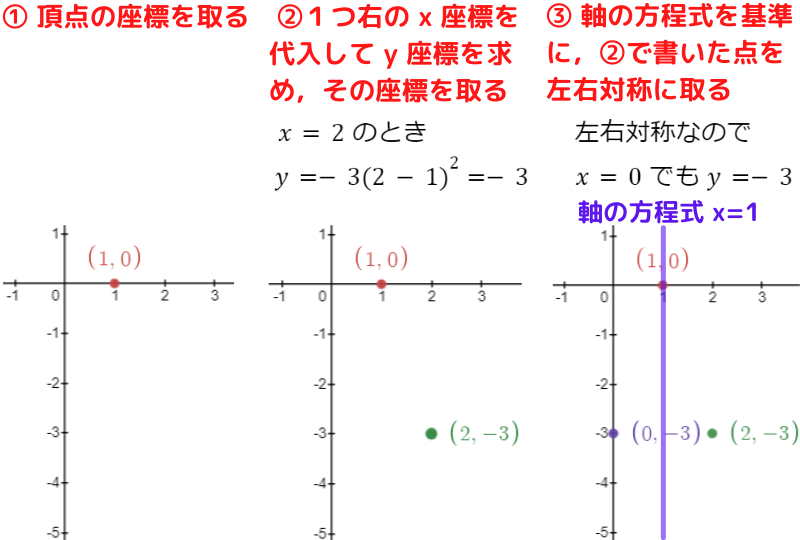
軸の方程式が x=1 だから，
x=1 を基準にして左右対称に点を取ればいいよ！
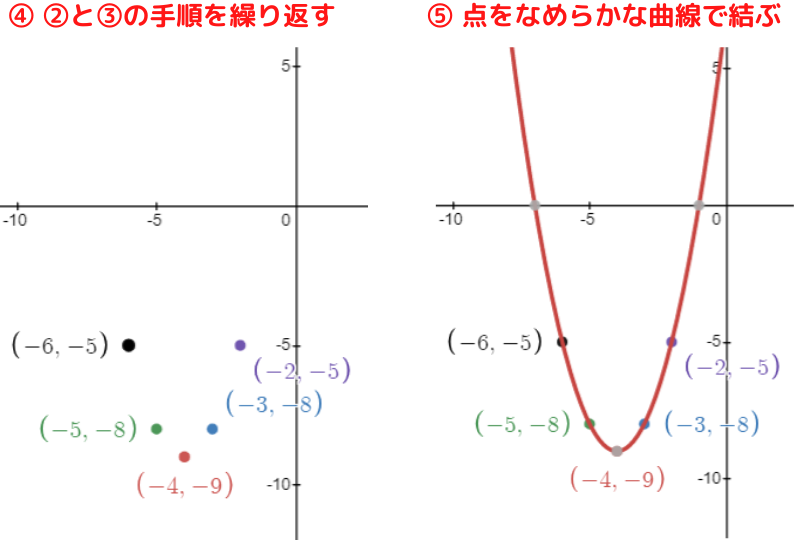
(4) y＝(x＋4)2 －9 軸の方程式 x＝－4 ，頂点の座標 (－4, －9)
軸の方程式が x=－4 だから，
x=－4 を基準にして左右対称に点を取ればいいよ！
軸の方程式と頂点の座標さえ分かれば，
２次関数のグラフを書くことは難しくないんだね！
★補足★ これで２次関数のグラフの書き方はすべて完璧？！
さてここまで，２次関数のグラフは全部で４種類と紹介しました
厳密に言えば，グラフの書き方が全部で４種類となります
実際には以下のように，頂点の座標がすぐには分からない形で与えられているケースも多いです
実はこの式，さきほど書いたグラフと同じ式になっています
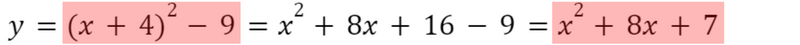
同じ式なのに，頂点の座標が分かる形と分からない形があるのです
頂点の座標が分からないと，グラフを正確に書くことができません
つまり，頂点の座標が分からない形の場合，頂点の座標が分かる形に式を変形する必要があるのです
頂点の座標が分かるように式を変形することを，平方完成といいます
平方完成については次回学習していきますね♪
それでは本時のまとめです
- 正確に２次関数のグラフを書くには❝５STEP❞を順番に進めればよい
- ２次関数のグラフは全部で４種類
- ２次関数のグラフはなめらかな曲線になるので，点と点をまっすぐ直線で結んではいけない
- 軸の方程式と頂点の座標が分かれば，２次関数のグラフを書くのは容易
- ２次関数の式は，頂点の座標が分かる形と分からない形がある
- 頂点の座標が分からない形の場合，平方完成をして頂点の座標が分かる形に式を変形する必要がある
次回，平方完成について学習します
どんな式の形をした２次関数でも，グラフが正確に書けるようにしていきましょう！
それでは今回は以上です。ありがとうございました
