madoryの『高校数学のブログ授業』です
- 数学を基礎から学び直したい高校生
- 高校入学前に予習して備えたい中学生
- 挫折した高校数学に再挑戦したい社会人
こんな❝あなた❞に向けて発信しています!
さっそく本時の結論です
「不等式は,両辺に負の数を掛けると不等号の向きが変わる!」
不等式とは,不等号を用いた式のことです
具体的には,『<,>,≦,≧』の4種類を用います
これら不等号を用いた不等式では,両辺に負の数を掛けると(もしくは割る)と不等号が逆向きになることに注意が必要です
この結論にしたがって,順番に見ていきましょう
まず,不等号の読み方・意味について押さえましょう

例えば,①は不等号の❝意味❞で読むと「x は 5 より小さい」となり,❝記号❞で読むと「x 小なり 5」となります
どちらの読み方をしていくのかは,担当の先生によって異なります
ちなみに,静岡市では意味で読む方が主流です
中学校でどちらで読んでいるかによるところが大きいため,地域差がありますね
一般には,意味で読むことの方が多いため,これ以降,本ブログでは❝意味❞で読ませていただきます
次に,不等式を計算する上で押さえておきたい,性質を確認します
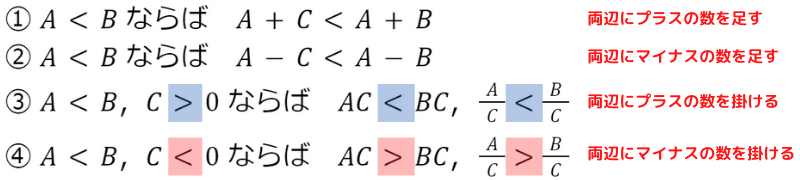

もともと『<(小なり)』だったのが,両辺にマイナスの数を掛けた④だけ,
『>(大なり)』に変わっているよ!

不等式は,両辺にマイナスの数を掛けた(割った)場合のみ,
不等号の向きが逆向きに変わるんだ!
不等式は,方程式(=)とほとんど同じように計算することができますが,一点だけ異なる部分があります
それは,『両辺にマイナスの数を掛ける(割る)と,不等号の向きが逆向きに変わる』点です!
唯一,気を付ける計算のルールと言ってもいいでしょう


ほんとだ~!!
両辺にマイナスの数を掛けたり割ったりすると,大小関係が変わるんだね!
マイナスの数を掛けることによって,左辺と右辺の大小関係が入れ替わるため,このような計算のルールが起こります
不等式の計算① 1次不等式
不等式の性質に注意し,1次不等式の計算を確認しましょう

不等式の性質で確認したように,加法・減法では不等号の向きは変わりません
つまり,移項しても不等号の向きは変わりませんね!
注意点は(2)…両辺にマイナスの数を掛ける(もしくは割る)ときに,両辺の大小関係が入れ替わるので,不等号の向きが変わります

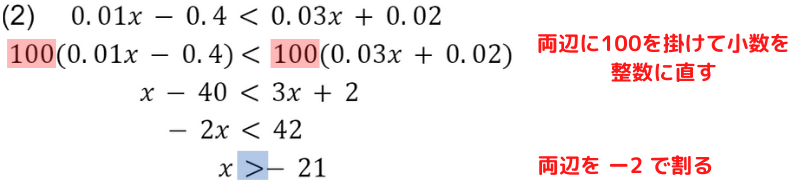

分数と小数の問題は,まず始めに整数に直すのがオススメだよ!
不等式の数直線への書き方
不等式は,数直線への書き方が決まっています
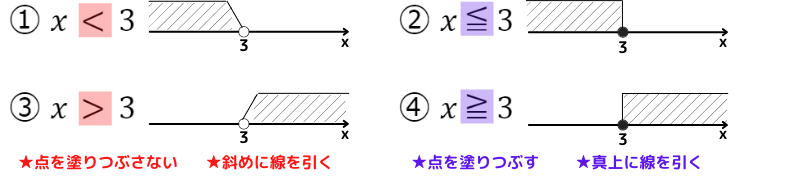

不等号に『=』があるかないかで,書き方が変わるんだね!
次の,連立不等式を解く際には,数直線への書き方を意識しましょう
不等式の計算② 連立不等式


連立不等式は,数直線を書いて重なった場所が答えになるんだね!



あれ? (3) は (2) のように2つの不等式に分けないの?

(3) のように,辺の真ん中にしか文字がない場合は,
2つの不等式に分けず,そのまま計算ができるんだ!
★補足★ 答えのない連立不等式
連立不等式は,2つの不等式を計算した後,その共通範囲を求めます
共通範囲がない場合について見ていきましょう


2つの数直線が重ならない場合もあるんだね!
実はこのように,連立不等式で答えがない問題(解はない)は簡単に作れます
問題としてふさわしいかは疑問であるため,目にすることは少ないですね
ただ,応用問題や入試問題まで進むと,計算過程で解がない場合はけっこう登場するので,理解しておく必要はあるでしょう
それでは本時のまとめです
- 不等号は❝意味❞で読むのが主流
- 不等式は,両辺にマイナスの数を掛ける(割る)と,不等号の向きが逆向きに変わる
- 1次不等式を計算する際は,マイナスの数を掛ける(割る)場合のみ注意
- 1次不等式を数直線上に書く場合,不等号に『=』がある or ないに注意
- 連立不等式は,2つの不等式を数直線に書き,重なった共通範囲が答え
- 真ん中の辺にしか文字がない連立不等式は,簡単に計算できる
- 答えのない(解のない)連立不等式もあり得る
基本的に,1次不等式で押さえておくルールは1つのみです
それは,『両辺にマイナスの数を掛ける(割る)と,不等号の向きが逆向きに変わる』点です!
これだけは絶対に忘れないように計算をしてくださいね!
今回は以上です。ありがとうございました
 サッカークロス
サッカークロス 

