madoryの『高校数学のブログ授業』です
- 数学を基礎から学び直したい高校生
- 高校入学前に予習して備えたい中学生
- 挫折した高校数学に再挑戦したい社会人
こんな❝あなた❞に向けて発信しています!
さっそく本時の結論から確認しましょう
「まず共通因数!次に公式!そして置き換えor式の整理!」
この順番で考えていくことです
因数分解は,公式を知らないと解くことができません
そこで,「しっかり公式を覚えて使うぞー!!」という発想になりがちです
もちろんこれ自体は正しいのですが,公式の前に考えることがあります
それが…❝共通因数でくくれないか❞考えることです!
共通因数でくくれない…そしたら因数分解の公式を考えましょう!
そしてそれでも解けない場合に,置き換えや式の整理を考えていきます
順番に見ていきましょう!
因数分解は,以下の4つの手順で行います
- 共通因数でくくれないか
- 因数分解の公式が使えないか
- 置き換えが使えないか
- 次数の低い文字で式を整理(文字2つ以上の場合)
展開は最終的に分配法則を使えば100%答えにたどり着けますが,因数分解はそうではありません!!
きちんと使いこなせるようにしましょう
手順① 共通因数でくくれないか
共通因数とは,各項(和の形で表される1つ1つ)に共通する因数のこと
いわゆる各項の共通部分です
すなわち,共通因数でくくるとは,同じ形を見つけてまとめる作業を指します
具体例を見てみましょう!
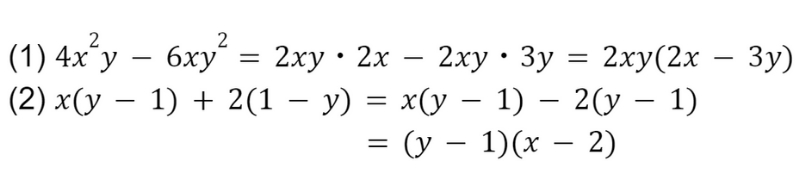

(2)は,(y-1) と (1-y) で符号違いになるんだね♪
違う形に見えるから見過ごさないようにしないと!!
因数分解で最初に勉強するのがこの共通因数
しかし,最も注意が必要なのも共通因数です!!
(2) の問題のように,一見同じ形に見えないものもあります
因数分解の学習を進めていくと,ついつい共通因数を見逃しがちになるので気を付けましょう
手順② 因数分解の公式が使えないか
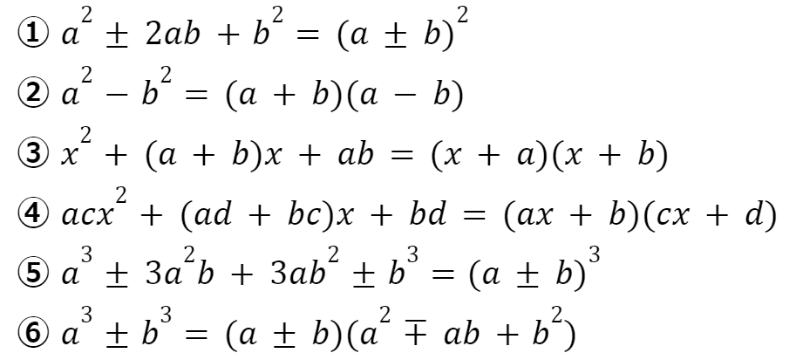

すべて展開の公式と左右が逆だね!
①~③は中学校で学習済みの公式,⑤⑥は「数学Ⅱ」の科目で再度学習するので,④を確認しましょう
④の公式を用いた因数分解の方法は,『たすき掛け』と呼ばれています!
箱根駅伝をイメージしてもらえるといいでしょう
箱根駅伝では,肩に❝斜めに掛けた❞各大学の襷(たすき)を,次の走者につないでいきますよね?!
一方,『たすき掛け』の計算では,数字を❝斜めに掛ける❞計算があります
どちらも❝斜めに掛ける❞からたすき掛けと呼ばれています
ちょっとしたダジャレですね笑
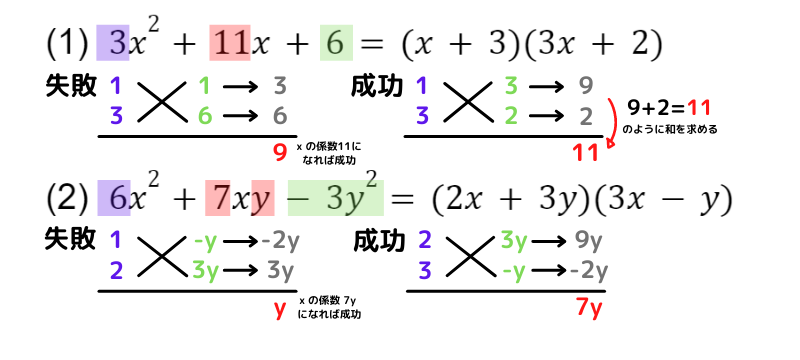

赤い部分の数字が一致すれば成功なんだね!
因数分解の公式は,この『たすき掛け』を用いた問題を確実にマスターしましょう!
手順③ 置き換えが使えないか
手順①&手順②ができなかったら,次に置き換えが使えないか考えましょう
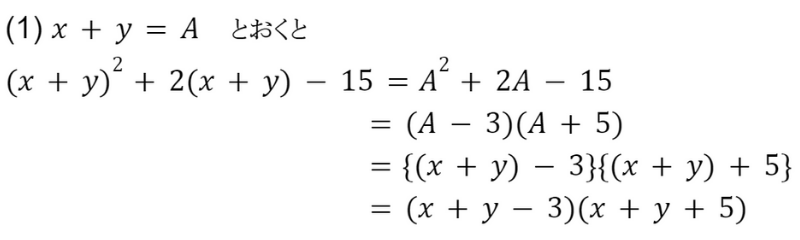
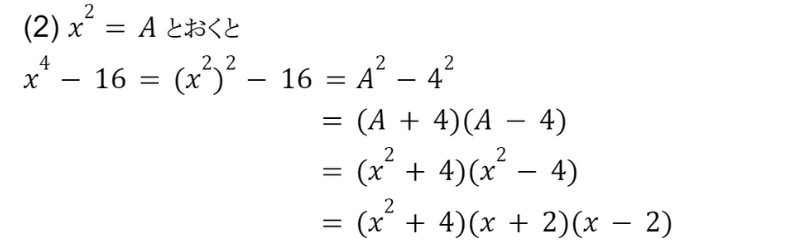

(2) はx4 だから4次式の因数分解だよ!
置き換えを利用することで,4次式でも因数分解できるケースもあるよ♪
手順④ 次数の低い文字で式を整理(文字2つ以上の場合)
複数の文字が式に含まれている場合,ある文字で式を整理します
正しくは,降べき(こうべき)の順に式を整理すると言います
降べきの順とは,ある特定の文字の個数が多いものから順に,式をまとめてある状態を指します


文字の個数が同じものは,かっこ( )を使ってまとめるんだね!

反対の意味で,昇べき(しょうべき)の順という言葉もあるよ
昇べきの順に整理することは,ほとんどないけどね~
それでは,式を整理して因数分解するケースを確認していきましょう!
(1) x2+xy+x+2y-2 (2) 2x2+5xy+3y2+2x+y-4
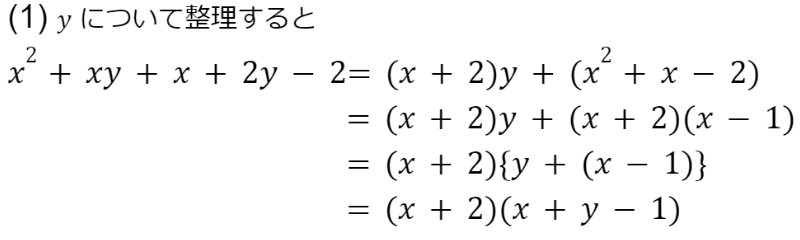
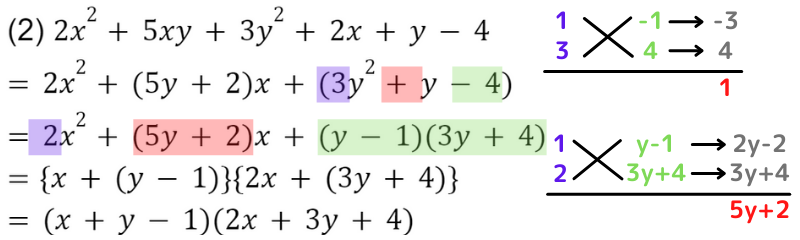

(2) は x について式を整理しなくてはいけないの??

(2) は x と y どちらも2次式(最大2乗)だから、どちらの文字で式を整理してもいいよ!
複数の文字がある場合は,次数の低い文字で式を整理しましょう
次数とは…最も掛けた文字の最大の個数 のことです
つまり,最大の文字の個数が少ない文字で,式をまとめていきます
(2) のように,最大の文字の個数が同じ場合については,どちらの文字で整理しても構いません
★補足★ 次数が同じでも整理の仕方によっては解けない問題
手順④の(2) の問題では,次数が同じであればどちらの文字で式を整理しても構わないと伝えました
しかし…実は次数が同じでも整理の仕方によっては解けない問題が存在するのです!!


なんと!!?
y について式を整理すると因数分解できないんだ…
【考え方1】は y について式を整理したけれど,計算が行き詰ってしまいました
【考え方2】は x について式を整理したら,最後まで因数分解することができました
このように,次数が同じでも整理の仕方によっては解けない問題が存在します
あえてポイントを挙げると,「次数が同じ場合は,文字の個数が少ない方で式を整理する」ことです
もしくは,「一方の文字で因数分解できなければ,もう一方の文字で式を整理してみる」
このように理解しておくのがいいでしょう!
最後に本時のまとめです
- まず共通因数!次に公式!そして置き換えor式の整理!
- 因数分解の公式は,『たすき掛け』をマスターしよう
- 式の整理は,次数の低い文字で!次数が同じ場合,一方の文字だと解けない場合も…
因数分解は,ルールを知らないとたどり着けません
一種のゲームみたいなものですね!
そして,因数分解を計算の途中で使うケースは本当にとっても多く,計算の土台と言っても過言ではありません!!
必ず使いこなせるようにしましょうね♪
今回は以上です。ありがとうございました
 サッカークロス
サッカークロス 

