【集合と命題⑧】対偶を用いた命題の証明

madoryの『高校数学のブログ授業』です

数学を基礎から学び直したい高校生
高校入学前に予習して備えたい中学生
挫折した高校数学に再挑戦したい社会人

こんな❝あなた❞に向けて発信しています！

本時の授業

【結論】命題『～ならば～である。』の証明は，対偶の利用を考えよう！

さっそく本時の結論です

「命題『～ならば～である。』の証明は，対偶の利用を考えよう！」

これまで【集合と命題】の単元の学習を進めてきました

最後に待ち構えているのは…，❝証明❞問題です！！

証明はちょっと…そんな声が聞こえてきそうですが大丈夫です！

本ブログの授業で，命題について理解できたあなたならもう一息です

それではさっそく，結論にしたがって，順番に見ていきましょう

対偶を利用した命題の証明

数学の世界には，もう数えきれないほどの証明問題，その手法があります

名だたる数学者の研究の歴史によって積み上げられた，人類の財産とも言えますね

あなたが使用している数学の公式（定理）は，成り立つことを証明した数学者のおかげで利用することができています

今回は，証明方法の１つ目…対偶を利用した証明方法を紹介します！

なぜ，対偶を利用して証明ができるのか？

対偶とは，ある命題に対して，逆かつ裏の命題を指しました

ある命題を，前後逆かつ意味の否定をすることで，対偶になりましたね！

詳しくは過去の授業を参考にしてください

2021年12月3日【集合と命題⑦】命題の逆・裏・対偶

今回証明をする上で大事なのは次の点です

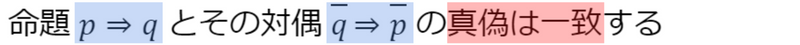
命題の真偽と対偶の真偽は一致するので，

もとの命題を証明すること
その対偶を証明すること

上記２点は，まったく同じ意味になります

対偶を利用した命題の証明　①基本編

それでは対偶を利用した命題の基本的な証明を，さっそく見ていきましょう

対偶を利用した命題の証明　①基本編

ホッくん

今回の問題は，もとの命題では証明することができないよ！

レッサーくん

本当だ！！

だから対偶を利用して証明するんだね♪

ホッくん

『～ならば～である。』の証明は，

対偶を利用するケースが多いよ！

今回の命題は，もとの命題では証明することができませんでした

そんなときに対偶の出番です！！

『～ならば～である。』命題の証明は，対偶を利用することを考えましょう！

対偶を利用した命題の証明　②応用編

証明の中に場合分けが必要となる，応用編の証明です

対偶を利用した命題の証明　②応用編

ホッくん

3 の倍数でない数を 3k+1, 3k+2 で表すことがポイントだよ！

★補足★　倍数と倍数でない数

証明の中で，奇数や偶数，3の倍数，3の倍数でない数と，様々な数を取り扱いました

ここでは，倍数と倍数でない数をまとめてみましょう！

倍数と倍数でない数

k を整数とする。

① ２の倍数（偶数）	2k	①′ ２の倍数でない数（奇数）	2k+1
② ３の倍数	3k	②′ ３の倍数でない数	3k+1, 3k+2
③ ４の倍数	4k	③′ ４の倍数でない数	4k+1, 4k+2, 4k+3
④ ５の倍数	5k	④′ ５の倍数でない数	5k+1, 5k+2, 5k+3, 5k+4