こんにちは,madoryです!

友達の誕生日をお祝いしようと思って,
折り紙でいろんな大きさの三角形を作ってるんだ♬


折り紙で作る❝ガーランド❞だね!

友達と協力して作ろうと思っているんだけど,
三角形の大きさをうまく言葉で伝えられないんだ…。

折り紙にもいろんな大きさがあるから同じ大きさで作りたいんだね!
三角形の辺の長さと角度を伝えてあげればいいんじゃない?

それが困ったことに,
定規はあるけど分度器がないから角度を伝えることができないんだ…。

なるほどね!じゃあ今日は,
三角形の辺の長さから角度を求めることができる
『余弦定理』を紹介するね!!
あなたは普段から❝定規❞は持っていても,❝分度器❞は持っていませんよね??
そうすると,長さを測ることはできても,角度を測ることはできませんね
そこで本時は,三角形の辺の長さから角度を求めることができる『余弦定理』を紹介します!
レッサーくんは三角形の辺の長さから角度を求めて,友達にきちんと伝えることができるのか??
さっそく授業をスタートしましょう♬
『余弦定理』を用いて,三角形の辺の長さから角度を求めよう!
さっそく本時の結論です
余弦定理を使う際のポイントは,2辺とその間の角 or 3辺

そもそも余弦って何?
三角比において,余弦とは cos を表しました
- 正弦(せいげん)‥‥ sine(サイン)
- 余弦(よげん)‥‥ cosine(コサイン)
- 正接(せいせつ)‥‥ tangent(タンジェント)
詳しくはこちらの記事を参考にしてください
 【図形と計量①】あなたはどれ派?三角比の定義の暗記方法3選
【図形と計量①】あなたはどれ派?三角比の定義の暗記方法3選
つまり余弦定理とは,ずばり『cos を用いた定理』となりますね!
余弦定理とは?公式の紹介
それでは余弦定理を紹介しましょう


なんだか難しそうな式が並んでいるね…

1つ式を覚えれば,あとは a,b,c を入れ替えるだけだよ!
余弦定理は一見難しそうな公式に感じると思います
けれど実際には『 a2=b2+c2-2bc cosA 』の式だけを覚えればOKです!
なぜならば,あとの2式は a,b,c を入れ替えただけだからです!
余弦定理の証明
余弦定理がどのように成り立つのか証明を見ていきましょう
まず,△ABC の A が鋭角の場合について考えていきましょう
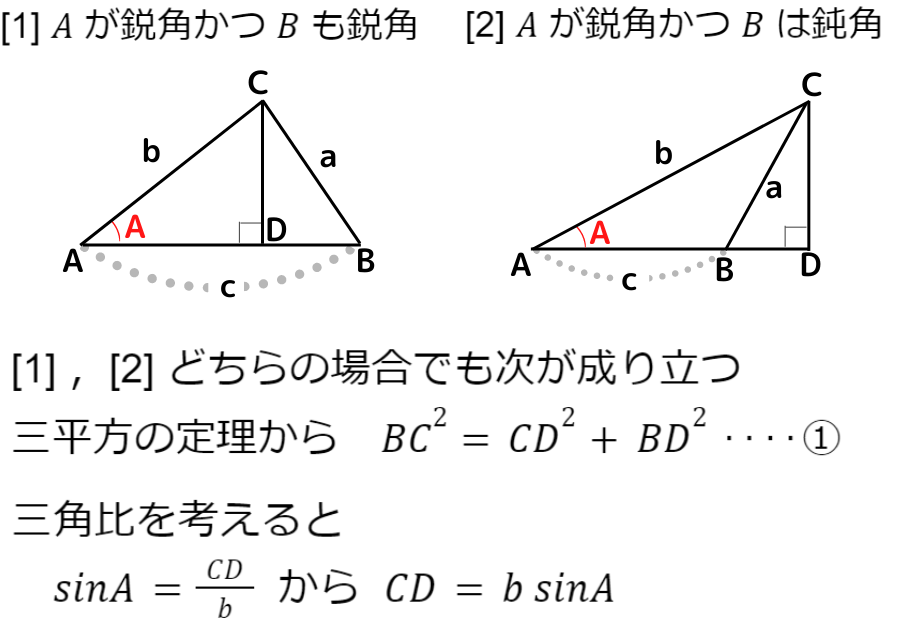
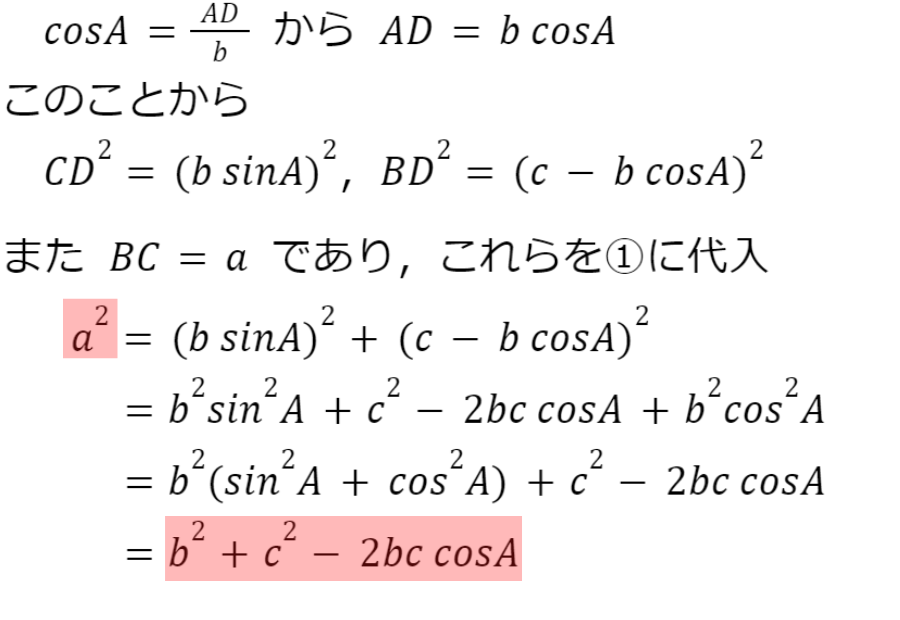
この証明は,△ABC の A が直角,鈍角の場合についても成り立ちます
本時では基本となる鋭角の証明のみにとどめます
また,あとの2式は a,b,c を入れ替えただけなので,余弦定理は1つ成り立てば残り2つの式も成り立つことが言えます

とっても長い計算で複雑だよ…

よく見ると『三平方の定理』『三角比の定義』『三角比の相互関係』と,
これまで学習してきた組み合わせで証明されているよ♬
余弦定理を用いた問題【①2辺とその間の角】


余弦定理の基本は,2辺とその間の角から残り1辺を求めることだよ!
余弦定理の基本の使い方は,三角形の2辺とその間の角を利用して,残り1辺を求めることです
『2辺とその間の角』または『2辺と挟む角』,もしくは『2辺挟角(きょうかく)』と理解しておきましょう
もう1問,余弦定理の基本問題を見ていきましょう


a でも b でも c でも,2辺とその間の角が分かれば残り1辺が求まるんだね♬
このように余弦定理で使用する角は,鋭角・鈍角にかかわらず公式を用いることができます
余弦定理の変形
余弦定理の基本は,2辺とその間の角から残り1辺を求めることだとお伝えしました
実は,余弦定理で求めることができるのはそれだけではありません!!
三角形の3辺の長さから角度を求めることができるのです!
そのために,余弦定理の公式を変形しておきましょう

まとめると,次が成り立ちます

三角形の3辺の長さから角度を求めるときは,この変形された余弦定理を使いましょう
余弦定理を用いた問題【②3辺】
それでは,余弦定理を変形した式を用いて,三角形の3辺の長さから角度を求めていきましょう
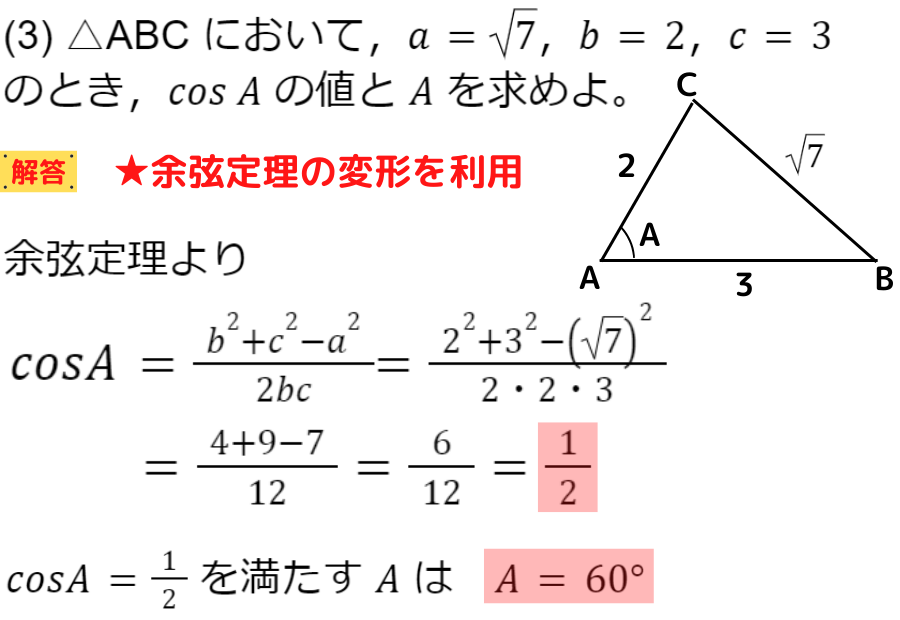

このように3辺の長さから角度を求めることができるのが,
余弦定理の特徴でもあるんだ♬
余弦定理は三角形の3辺の長さから角度を求めることが可能です
これは余弦定理の大きな特徴とも言えますね!

レッサーくん!
この計算を使えば定規で3辺の長さを測って角度を計算することができるよ♬

よかった!!
これで折り紙を使ったガーランドを作るときに,
友達に三角形の角度を伝えることができるよ♬
これで無事にレッサーくんの悩みも解決できそうですね!!
★補足★ 直角三角形の場合の余弦定理ってどうなるの??
今回紹介した余弦定理の証明はAが鋭角のみでしたが,Aが直角,鈍角の場合も成り立ちます
さて,Aが直角の場合の余弦定理って,いったいどうなるんでしょう??
Aが直角の場合の問題を1つ見ていくことにしましょう


あれ,待って!!
直角三角形だから三平方の定理で a は求まるんじゃない?!

そうだね!!
余弦定理と三平方の定理を比較してみようか!
Aが直角の場合には,余弦定理ではなく三平方の定理で a の長さを求めることができます
余弦定理と三平方の定理を並べてみましょう


えっ!!
三平方の定理って余弦定理の一部だったの!!?

その通り!
直角三角形でしか使えない三平方の定理を,
常に使えるようにしたのが余弦定理ともいえるね♬
さきほどの問題を三平方の定理でも解いてみました
そして公式として比較してみてみると,三平方の定理が余弦定理の一部であることが見えてくるでしょう
三平方の定理は直角三角形でしか用いることはできません
一方、余弦定理は直角に限らず,鋭角,鈍角と,どんな角度の三角形でも用いることができます
つまり『余弦定理は三平方の定理の上位互換』と見ることができるでしょう!
また別の見方をすると,『余弦定理は三平方の定理の過不足分を調整した公式』と考えることもできますね!

それでは本時のまとめです
- 余弦とは cos のこと。つまり余弦定理とは cos を用いた定理
- 余弦定理は3式あるが,文字を入れ替えただけなので1式だけ覚えればよい
- 余弦定理の基本は,2辺とその間の角から残り1辺を求めること
- 余弦定理は変形して,3辺の長さから角度を求めることができる
- 実は三平方の定理は余弦定理の一部。余弦定理は『三平方の定理の上位互換』もしくは『三平方の定理の過不足分を調整した式』といえる
本時は余弦定理について学習してきました
まず三平方の定理と違って,余弦定理は直角に限らずどんな三角形でも用いることができました
余弦定理の基本は2辺とその間の角から残り1辺を求めること
また,3辺の長さから角度を求めることができること
これらを問題で活用できるようにしてくださいね!
今回は以上です。ありがとうございました
 サッカークロス
サッカークロス 

