こんにちは,madoryです!

最近,日本平動物園の近くで富士山型のコーンを見かけるんだ!!


この可愛い富士山型のコーン…,
実は,地元静岡県富士宮市の会社が作っているんだよ♬

そうだったんだ~!
静岡県と言えば富士山だから,見るとなんだか嬉しい気持ちになるね♬

じゃあ今日は,
富士山コーンの形である❝三角形❞で成り立つ公式について,
一緒に勉強していこうか♬
本時は三角形で成り立つ公式『正弦定理』について学習していきます
三角比は直角三角形で成り立つルールでしたが,本時で学習する『正弦定理』は直角三角形である必要はありません!
どんな三角形でも成り立つ…そんな新しい公式について楽しく勉強していきましょう♬
ということで本時は,
三角形で成り立つ公式『正弦定理』について理解しよう!
さっそく本時の結論です
正弦定理を使う際のポイントは,外接円の半径Rを含むか含まないか

そもそも正弦って何?
三角比とは sin,cos,tan のことであり,そのうち正弦とは sin を表しました
- 正弦(せいげん)‥‥ sine(サイン)
- 余弦(よげん)‥‥ cosine(コサイン)
- 正接(せいせつ)‥‥ tangent(タンジェント)
詳しくはこちらの記事を参考にしてください
 【図形と計量①】あなたはどれ派?三角比の定義の暗記方法3選
【図形と計量①】あなたはどれ派?三角比の定義の暗記方法3選
つまり正弦定理とは,ずばり『sin を用いた定理』となりますね!
正弦定理とは?公式の紹介
さっそく正弦定理を紹介しましょう!
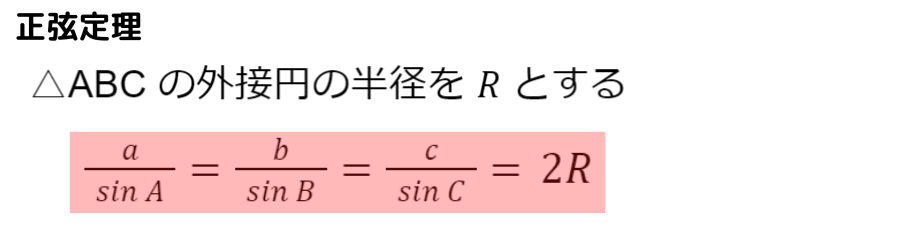
正弦定理は,三角形ABC の辺の長さと大きさ,外接円の半径を用いた公式です
さらに,大文字で表される角度Aと小文字で表される辺の長さ a は,三角形の角度とその向かい合う辺の関係性です

A → B → C と順に進んでいくから覚えやすいね!
正弦定理の証明
次に,正弦定理の成り立ちを紹介していきましょう
いわゆる❝証明❞ですね!

証明することで,納得して公式を使うことができるね♬
まず,三角形の3つの頂点を通る円を外接円といいます
△ABC の外接円の半径をRとして,A が鋭角の場合について考えていきましょう
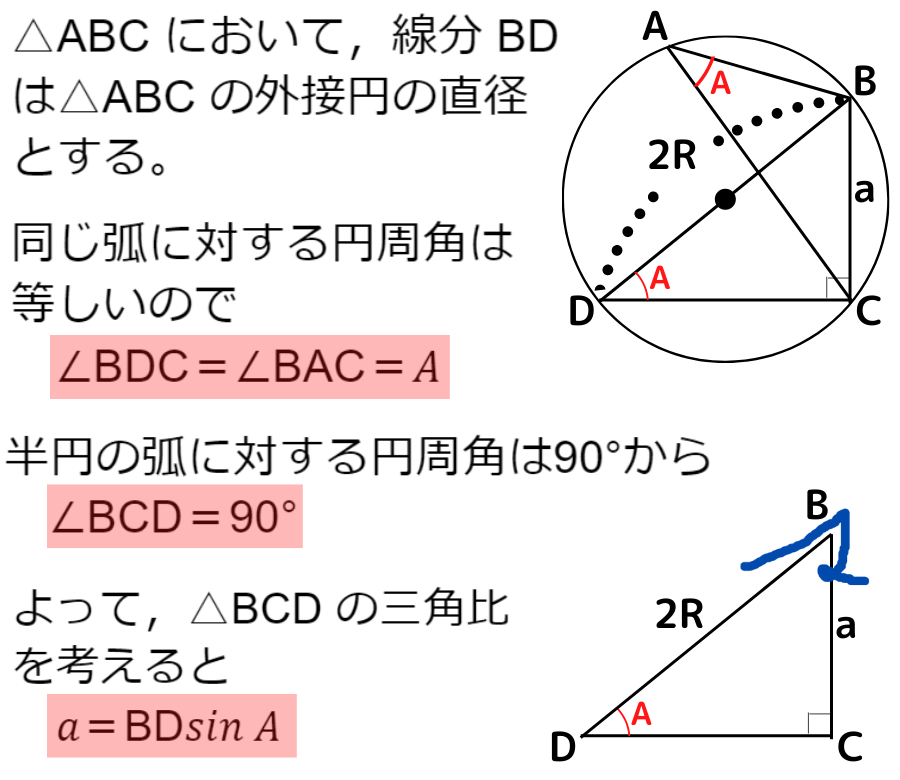


中学校で学んだ円周角と,高校で学んだ三角比を組み合わせて証明できるね!

本当だ!!難しいけれど…なんとか理解できたよ♬

実際には,Aが直角の場合と鈍角の場合も考えて,完全に証明できるね!
ここではAが鋭角の場合について証明をしました
実際にはAが直角の場合と鈍角の場合も証明して,どんなAの角度についても正弦定理が成り立つことを示す必要があります
正弦定理を使って問題を解く際に,証明を意識することはないと思いますので,Aが直角と鈍角の場合は省略します
しかし,教科書に載っているような証明を理解しておくことは大事ですね!
様々な問題を複合して考える練習になりますよ♬
正弦定理を用いた問題【①外接円の半径Rを含む】
正弦定理を用いた問題は,外接円の半径Rを含むか含まないかで,大きく2種類の解法に分かれます
まずは外接円の半径Rを含む解法について見ていきましょう!


まずは王道!
外接円の半径Rを求めることができたね‼


外接円の半径Rを利用して,三角形の角度を求めることができたね!
正弦定理の公式において,外接円の半径Rを含む場合についてまとめておきましょう
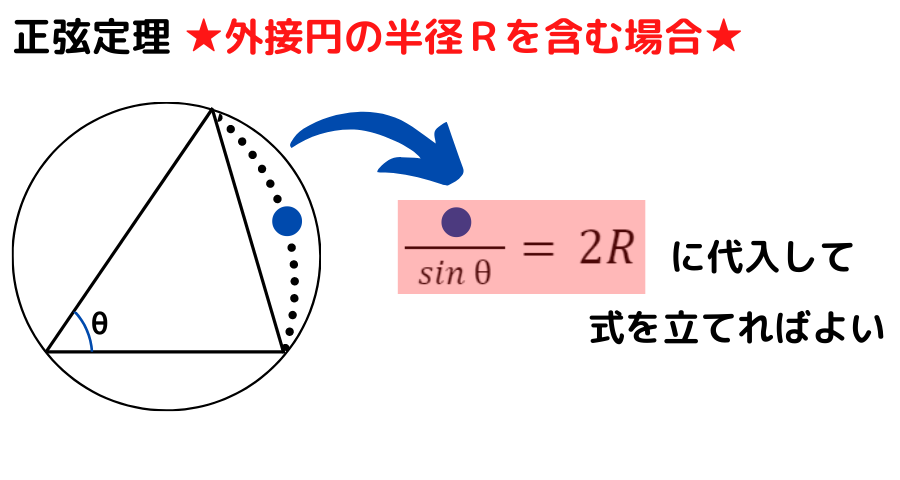
正弦定理を用いた問題【②外接円の半径Rを含まない】
次に,外接円の半径Rを含まない場合の正弦定理の公式の用い方について,見ていきましょう


式の中に外接円の半径Rが登場しなくなるよ!
外接円の半径Rを含まない場合についてまとめましょう
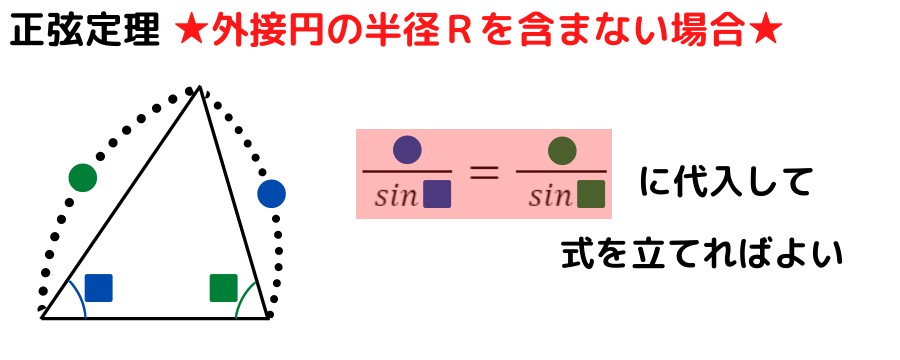

なるほど!!
外接円の半径Rを含まない場合は上の式に当てはめればいいんだね♬
★補足★ 直角三角形で正弦定理を用いると…どうなる??
正弦定理を使う際に考える三角形は,直角三角形である必要はありませんでした
仮に,直角三角形だった場合を考えてみることにしましょう!
直角三角形の場合を正弦定理を用いて解いてみます


『sin 90°=1』だったね!

直角三角形の場合でも正弦定理を用いて解くことができるね♬
でも…実は別解があるんだよ!!
次に,同じ問題を別解で解いてみます!
三角比の定義を用いた方法です


そっか!!
直角三角形だから三角比の定義で解くことができるんだね♬

その通り!!
三角比って便利でしょ^^
直角三角形の場合は,正弦定理で問題を解くこともできますが,あえてその必要はありません
三角比の定義を使うことで,より簡単に解くことができます
直角三角形の場合は,正弦定理でなくまず三角比の定義を考えるようにしてくださいね!
それでは本時のまとめです
- 正弦とは sin のことであり,正弦定理とは sin を用いた公式
- 正弦定理の証明は,鋭角・直角・鈍角の場合に分けて考える。鋭角の場合の証明は,円周角の定理と三角比の定義を用いる
- 正弦定理の使い方は,外接円の半径Rを含むか含まないかで判断する
- 正弦定理を用いて三角形の辺の長さや角度を計算できる
- 直角三角形の場合も正弦定理を用いることはできるが,三角比の定義を用いるとよい
本時は正弦定理に関して詳しく解説をしてきました
いかがだったでしょうか?
❝正弦定理❞というと,なんだか堅苦しく抵抗感を覚えやすいものです…
しかし,外接円の半径Rを含むか含まないかで仕分けをして考えることで,解法が2種類に枝分かれします
本時の授業を通して,迷わず式を立てることができるようになれば幸いです
今回は以上です。ありがとうございました
 サッカークロス
サッカークロス 

