こんにちは,madoryです!

レッサーくん!!
魅力たっぷりの三角比のこと,好きになってくれたかな?

うん!!ぼくはその中でも特に『tan(タンジェント)』が好きだな~!
❝タンジェント❞ってヒーローみたいでカッコいいもん♬

実は『sin』『cos』の値から『tan』の値を求めることができるんだよ!
今日はその勉強をしていこうね♬

えっ!?そうなの!!!
『sin』『cos』から『tan』の値を求めてみたいな♬
三角比とは,相似な直角三角形における3辺のうち,ある2辺を用いた値を指しました
同じ図形から考えられた値が三角比…こう考えると『sin』『cos』『tan』には密接な関係がありそうですよね?!
そう…実は,
「三角比の『sin』『cos』『tan』には関連性がある!」
のです!
本時では,この三角比の関連性を公式としてまとめた『三角比の相互関係』について学習します
さっそく本時の結論です
三角比の相互関係を用いて,1つの三角比の値から残り2つの三角比の値を求められる!
三角比の相互関係とは?
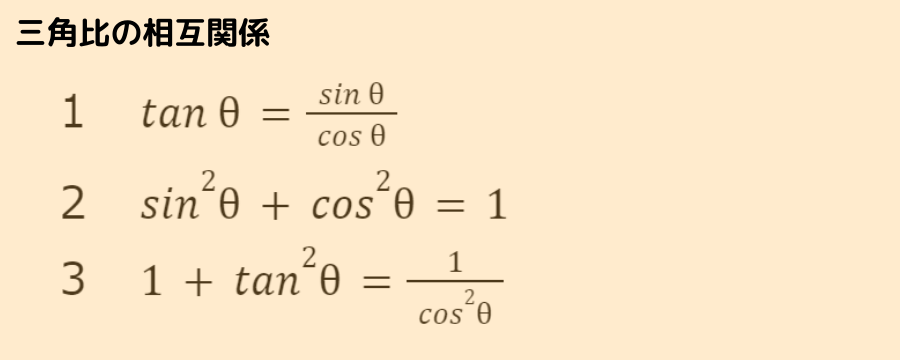

『三角比の相互関係』の公式についてまとめておきましょう
- 公式1番は,『sin』『cos』『tan』の三角比3つすべてを使用し,2乗がつかない
- 公式2番・3番は,『sin』『cos』『tan』の三角比3つのうち2つを使用し,2乗がつく

それにしても複雑な公式だね…
どうやってこの公式が作られたの?

これまで勉強してきた『三角比の定義』や『三平方の定理』から作られるんだ!
作り方(証明)を見ていこうね♬
三角比の相互関係はどうやって作られる?(証明)
『三角比の相互関係』の公式がどうやって作られるのか,その証明を見ていきましょう


本当だ!!
『三角比の定義』と『三平方の定理』を使っているね!
三角比の相互関係:例1


『sin』の値から『cos』『tan』の値を求めることができたね!

同じように計算すれば,
『cos』の値からも『sin』『tan』の値を求められそうだよ!
『sin』の値から『cos』『tan』の値を求める場合は,三角比の相互関係の公式を【2番→1番】の順に使用します
『cos』の値から『sin』『tan』の値を求める場合も同様に,三角比の相互関係の公式を【2番→1番】の順に使用していきます
三角比の相互関係:例2


今度は『tan』の値から『sin』『cos』の値を求めることができたね!
『tan』の値から『sin』『cos』の値を求める場合は,三角比の相互関係の公式を【3番→1番】の順に使用します
三角比の相互関係のまとめ
1つの三角比の値から,残り2つの三角比の値を求める方法をまとめましょう
- 『sin』 → 公式2番『cos』 → 公式1番『tan』(公式3番も可能)
- 『cos』 → 公式2番『sin』 → 公式1番『tan』(公式3番も可能)
- 『tan』 → 公式3番『cos』 → 公式1番『sin』(公式2番も可能)
前半は公式2番 or 3番を使用して,後半は常に公式1番を使用すればよいことが分かりますね!
ちなみに,後半は公式1番でなくても計算は可能です
ただ,公式2番と3番は2乗の計算が含まれるため,2乗を外すときに注意する必要があるので,後半の計算では公式1番を使用するのがおすすめです!
★補足★ 図形を用いた簡単な計算を紹介
実は,1つの三角比の値から残り2つの三角比の値を求める,別の方法が存在します!!
それが図形(直角三角形)を用いた方法です
さきほど計算した2問を,別の方法で解いてみましょう

図形を用いた別の方法を紹介するね♬
こっちの方法の方が簡単に感じると思うよ!


すごい!!図形を用いると三平方の定理で簡単に計算できるんだね♬

図形を用いた方法を整理しましょう
- 三角比の定義(筆記体)から直角三角形の2辺を記入する
- 直角三角形の残り1辺を三平方の定理から求める
三角比の相互関係で解くのか,図形を用いた別の方法で解くのか,両方解けるようにしておいて問題によって選択できるといいですね!
それでは本時のまとめです
- 『三角比の相互関係』は公式3つ
- 公式1番は三角比3つすべて使用し,2乗がつかない
- 公式2番・3番は三角比2つを使用し,2乗がつく
- 三角比の相互関係は,『三角比の定義』と『三平方の定理』から作られる
- 三角比の相互関係の公式を2つ使用して,1つの三角比の値から残り2つの値を求められる
- 1つの三角比の値から残り2つの値を求める別の方法として,図形を用いた方法がある
本時は三角比の相互関係について学習をしてきました
三角比の相互関係を用いることで,1つの三角比の値から残り2つの三角比の値を求めることができるようになりましたが,実はまだまだ三角比の相互関係には使い道があります
今後の学習を楽しみにしてくださいね!
今回は以上です。ありがとうございました
 サッカークロス
サッカークロス 

