サッカークロス 
madoryの『高校数学のブログ授業』です
- 数学を基礎から学び直したい高校生
- 高校入学前に予習して備えたい中学生
- 挫折した高校数学に再挑戦したい社会人
こんな❝あなた❞に向けて発信しています！
本時は『２次関数の決定 part 2』です
『２次関数の決定 part 1』を先に学習してから本時に取り組むと理解しやすいと思うので，こちらを参考にしてください
【２次関数⑧】頂点・軸から式を求める｜２次関数の決定 part1
それではさっそく本時の結論です
「３点の座標を代入して，連立３元１次方程式を解け！」
与えられた３点の座標を式に代入して，連立３元１次方程式を解くことで，２次関数の式を決定することができます
では結論にしたがって，詳しく見ていきましょう
前時は，頂点・軸から２次関数を決定したね！
本時は，３点の座標から２次関数を決定するよ！
２次関数の式の形２選
２次関数の式の形には２通りの表記方法がありました
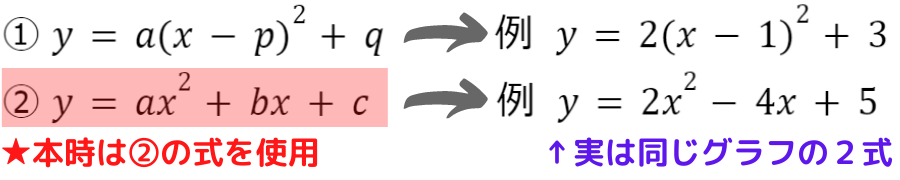
連立３元１次方程式の解き方
３点の座標から２次関数を決定する下準備として，連立３元１次方程式を紹介します
連立２元１次方程式が普段解いている連立方程式だね！
連立２元１次方程式はよく使うから，
略して❝連立方程式❞と呼んでいるんだ♬
３点の座標から２次関数を決定するためには，連立３元１次方程式の計算が欠かせません
その解き方を見ていきましょう
解き方のステップは３つです
- ｃを消去する（ｃを消去した式を２つ作る）
- ａとｂの連立方程式を解く
- ｃを求める（最も代入が簡単そうな式にａとｂを代入して計算する）
２次関数の決定『３点の座標から求める』
初めに３点の座標を代入すると，
連立３元１次方程式になるんだね！
★補足★ どっちの式の形で解く？
２次関数の式の形は以下の２種類がありました
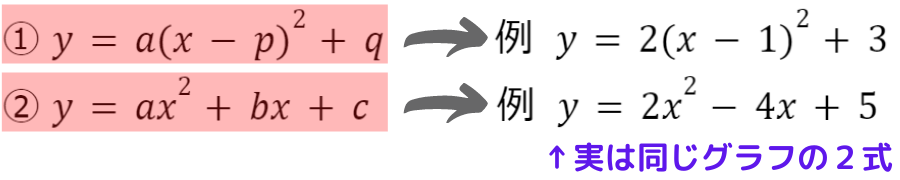
次の２問はどちらの式の形を利用して解くでしょう？
う～ん、複雑だ…
どっちも座標が与えられているけれど…
それぞれ解答を見ていきましょう
２つ目の式の形を使っているよ！
ａがすぐ決まり，あとは頂点ではない座標２点を代入するからだね♬
１つ目の式の形を使っているよ！
最小値＝頂点なので，頂点の座標が関係するからだね♬
上記２つの問題のように，頂点の座標（もしくは軸の方程式）が関係するのかしないかが，式の形を選ぶ判断基準になります
まとめると次の通りです
なるほど！
頂点の座標・軸の方程式が関係するかどうかで，
最初の式の形を選択すればいいんだね♬
それでは本時のまとめです
- ２次関数の式の形は２種類ある
- 普段よく計算している連立方程式の正式名称は「連立２元１次方程式」
- 連立３元１次方程式の解き方は３ステップ『①ｃを消去する ②ａとｂの連立方程式を解く ③ｃを求める』
- ３点の座標から２次関数を決定する際，連立３元１次方程式を解くことになる
- ２次関数の決定は，頂点の座標・軸の方程式が関係するかしないかで，式の形を選択して解く
本時は『２次関数の決定 part2 』として，３点の座標から２次関数の決定をする方法を紹介しました
連立３元１次方程式を解くことができればOKですね！
また，２次関数の決定は，頂点の座標・軸の方程式が関係するかしないかという判断基準で，問題を解くようにしていきましょう
今回は以上です。ありがとうございました
