サッカークロス 
madoryの『高校数学のブログ授業』です
- 数学を基礎から学び直したい高校生
- 高校入学前に予習して備えたい中学生
- 挫折した高校数学に再挑戦したい社会人
こんな❝あなた❞に向けて発信しています！
２次不等式は，以下の３ステップで解くと学習しました
①２次方程式を解いて，②下に凸のグラフを書き，③不等号４種類から解を判断!!
詳細は，過去の授業を参考にしてください
【２次関数⑬】グラフと不等号で解を判断！２次不等式の解き方３ステップ
本時では，グラフを利用せずにスピード重視で２次不等式を解く方法を紹介します！
さっそく本時の結論です
「２次不等式の解は全12パターン！判別式から計算しパターン化して暗記!!」
この結論にしたがって，順番に見ていきましょう
２次不等式の解“全12パターン“
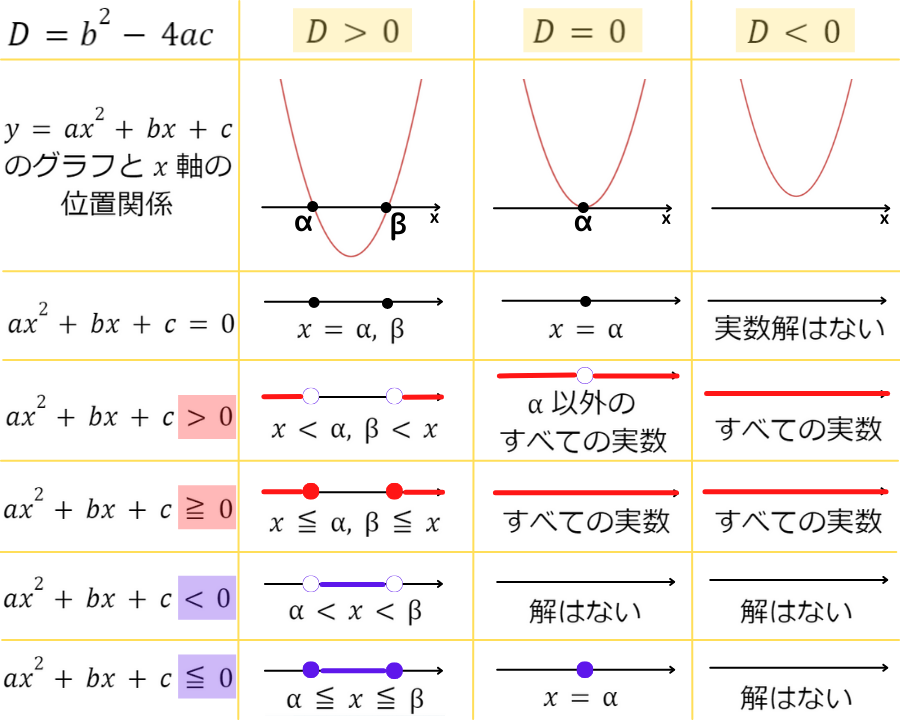
２次不等式の答えは12パターンもあって大変だ…
判別式の符号が分かれば，４パターンずつに絞れるよ！
さらに，Ｄ＜0 ならば答えは２パターンになるんだ♬
★スピード重視★２次不等式の解き方フローチャート
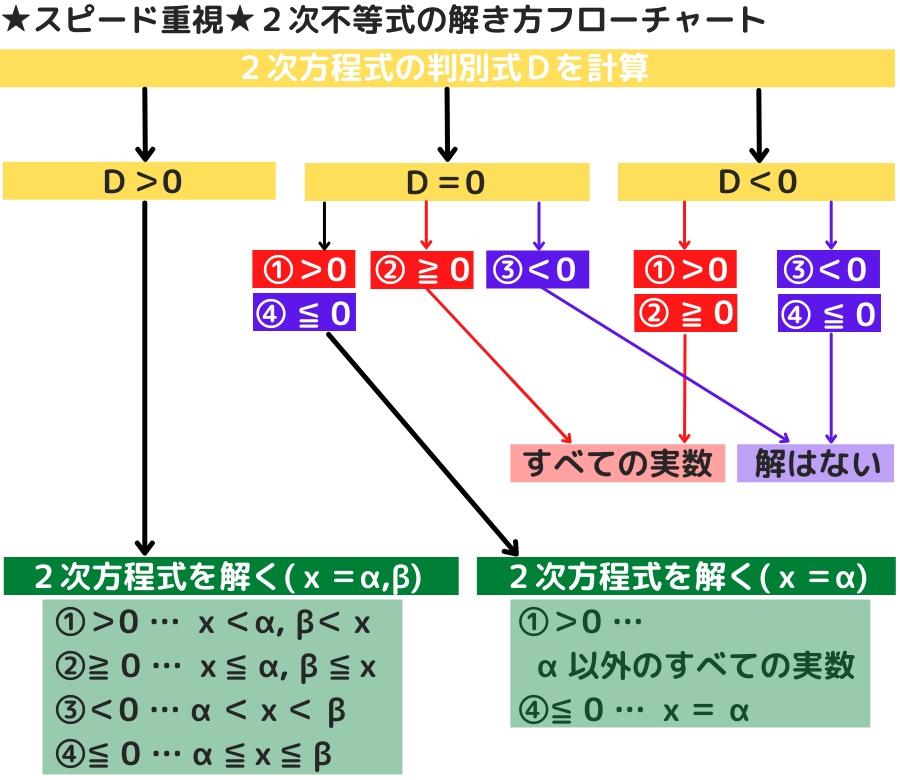
このフローチャートの流れを理解しておこうね！
★スピード重視★２次不等式の解き方【Ｄ＜０の場合】
判別式Ｄが負になるから，解は２択になるんだね♬
判別式Ｄ/4 が使えれば，もっと計算が簡単だね！
さらに，判別式の計算を書かずに頭の中でできると，
もっと計算スピードが早くなるよ！
★スピード重視★２次不等式の解き方【Ｄ＝０の場合】
Ｄ＝０のときも，
「すべての実数」or「解はない」の答えを
すぐに出せる場合があるよ！
Ｄ＝０のときは，
判別式のみで解ける場合と，
２次方程式を解かないといけない場合があるんだね！
★スピード重視★２次不等式の解き方【Ｄ＞０の場合】
判別式Ｄ＞０のときは，
常に２次方程式を解くようにすればいいよ！
２次方程式は，因数分解で解けなければ解の公式だね！
★補足★ 判別式を頭の中で計算すれば，２次不等式の解き方の半分６パターンは途中計算不要⁉︎
レッサーくん，判別式の計算は書かずに頭の中でできる？
書かずに計算したことはなかったけど…
意外と簡単だからできそうだよ♫
みなさんはお気づきでしょうか？
２次不等式の解き方は全部で12パターン，その半分の６パターンは判別式だけで答えを出せるのです！
判別式の計算は非常に楽であるため，頭の中で計算することも可能でしょう
…つまり，判別式を頭の中で計算すれば，２次不等式の解き方の半分６パターンは途中計算不要といえるのです！！
判別式を頭の中で計算できれば，
２次不等式の半分の６パターンは途中計算不要だよ！
それってすごいことだね！！
２次不等式って意外と簡単かも♫
判別式を頭の中で計算する場合の考え方について，整理しておきましょう
- 判別式を頭の中で計算
- Ｄ＝０かつ２次不等式『≧ ０』or『＜０』のとき，または Ｄ＜０ のとき，解は「すべての実数」or「解はない」の二択
- 上記以外の場合は，２次方程式を解く
それでは本時のまとめです
- ２次不等式の解は全12パターン，判別式の符号によって４パターンずつに分かれる
- ２次不等式はフローチャートで整理しよう！
- 判別式Ｄ＜０のときの解は，「すべての実数」or「解はない」
- 判別式Ｄ＝０のとき，『 ≧ ０』は「すべての実数」，『＜０』は「解はない」，それ以外は２次方程式を解く
- 判別式Ｄ＞０のとき，常に２次方程式を解く
- 判別式の計算を頭の中でできれば，全12パターン中６パターンは途中計算不要ですぐに答えを出せる
本時はグラフを使わずにスピード重視で解く２次不等式について学習しました
ポイントはフローチャートで全体像を理解しておくこと，判別式をなるべく頭の中で計算することです
早く，正確に解くことを意識して勉強を進めてくださいね！
今回は以上です。ありがとうございました
