madoryの『高校数学のブログ授業』です
- 数学を基礎から学び直したい高校生
- 高校入学前に予習して備えたい中学生
- 挫折した高校数学に再挑戦したい社会人
こんな❝あなた❞に向けて発信しています!
本時は2次不等式の解き方について学習します
2次式 かつ 不等式 ⇔ 2乗が入った不等式のこと
2次不等式は,今後多くの場面で必要となる重要な計算です
2次関数のグラフからイメージして解けるように学習していきましょう
ではさっそく本時の結論です
「①2次方程式を解いて,②下に凸のグラフを書き,③不等号4種類から解を判断!」
この結論にしたがって,順番に見ていきましょう
不等号4種類が示す場所
不等号は以下の4種類がありましたね!
- > ‥‥ 例 x>5(xは5より大きい)
- ≧ ‥‥ 例 x≧5(xは5以上)
- < ‥‥ 例 x<5(xは5より小さい)
- ≦ ‥‥ 例 x≦5(xは5以下)
それぞれの不等式は下の図の部分を表します
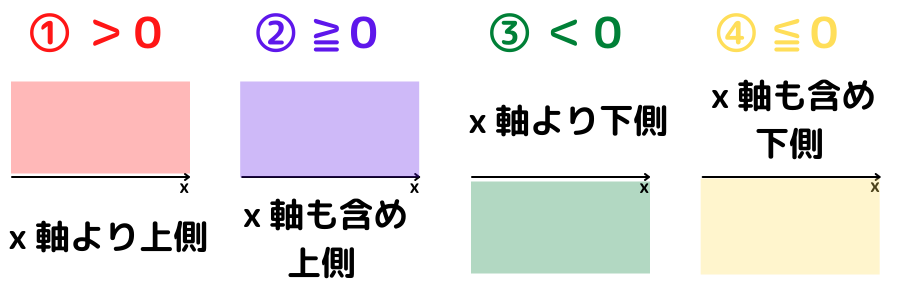

不等号4種類が示す場所をしっかりイメージしておこうね♬
2次不等式の解き方「2次方程式の解が2個⇔D>0」
2次不等式の解き方は次の3ステップです!
- まず2次方程式を解く
- 下に凸のグラフを書く
- 不等号4種類から解を判断
さっそく問題を見ていきましょう
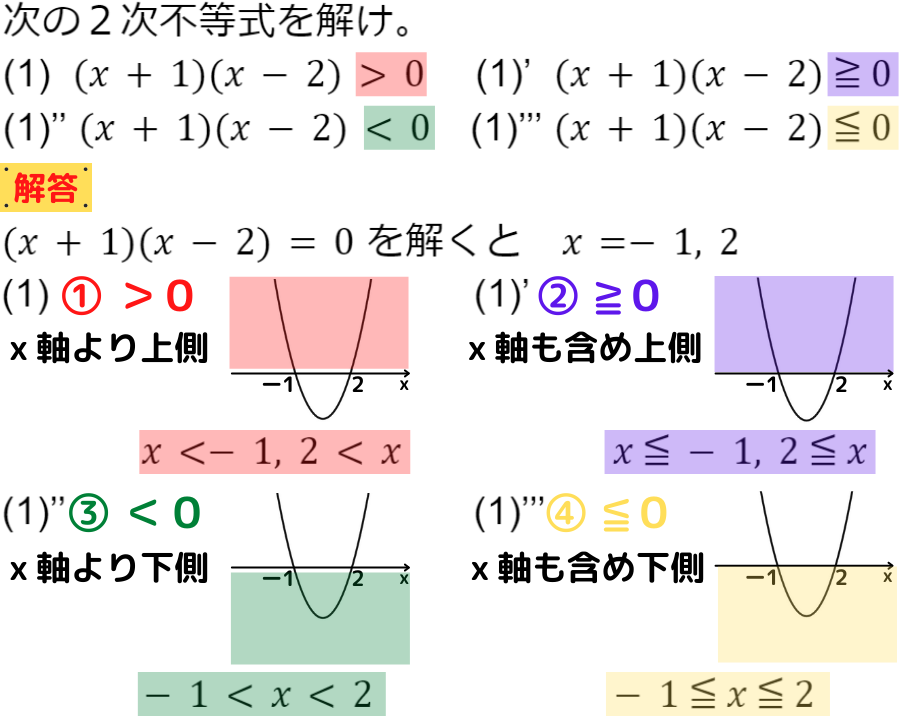

x軸を基準にして,上側なのか下側なのかが大事だよ!

不等号が4種類だから,解も4種類になるんだね!
2次不等式の解き方「2次方程式の解が1個⇔D=0」
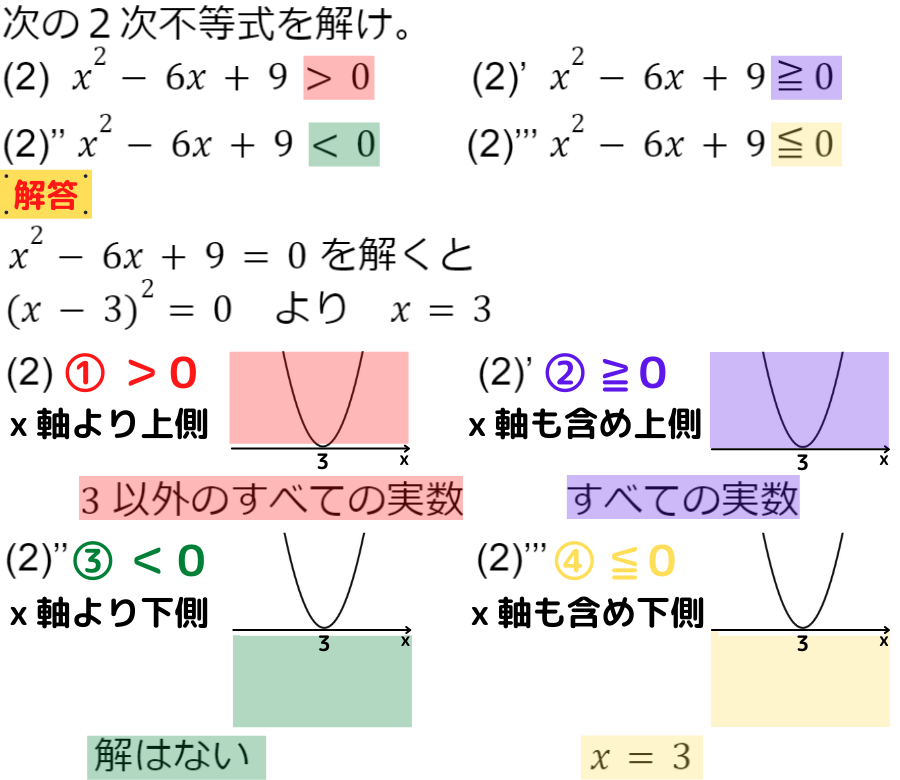

やはり解は4種類だね!
ただ,4種類全然違うからややこしい…‼︎
2次不等式の解き方「2次方程式の解が0個⇔D<0」
2次方程式を解くことができない場合を見ていきましょう

2次方程式が解けない
⇔ グラフがx軸と共有点をもたない(交わらない)
となるよ!
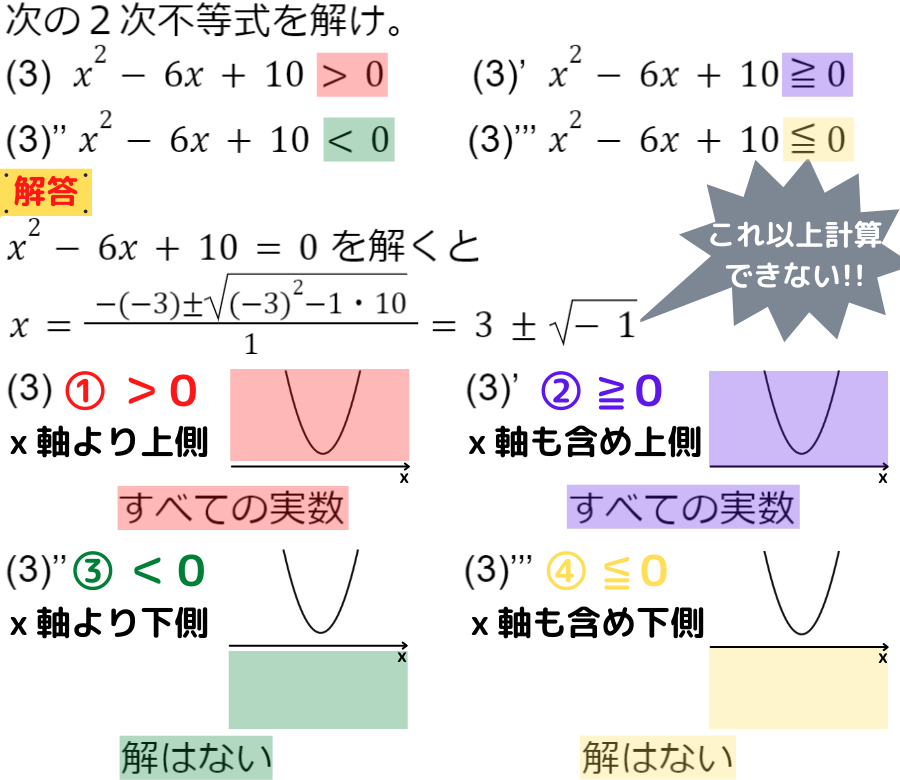

あれ…,解の種類が2種類だけだね!

そうなんだ!2次方程式の解がない場合だけ,
「すべての実数」or「解はない」の2択になるよ♫
★補足★ 上に凸のグラフはどう解けばいいのか?
2次不等式の解法は以下の3ステップでした
- まず2次方程式を解く
- 下に凸のグラフを書く
- 不等号4種類から解を判断
では,上に凸のグラフになる場合はどう解けばいいのでしょうか?
上に凸の場合のグラフを書けば解くことはできるのですが,少々ややこしくなるため,下に凸のグラフに直してから計算を考えていくのがおすすめです!
例を見てみましょう


両辺にー1を掛ければ下に凸のグラフになるんだね♬
不等号の向きが変わることに気を付けないと!!
もし,上に凸のグラフのまま計算したらどうなるのか…
こちらも確認してみましょう


上に凸のグラフのままでも計算できることが分かるね!

なんかややこしく感じる…。
ぼくだったら,両辺にー1を掛けて常に下に凸のグラフで考えたいな~
それでは本時のまとめです
- 2次不等式とは,2乗が入った不等式のこと
- 不等号は4種類。x軸を基準にして上側か下側かを考える
- 2次不等式の解き方は3ステップ! ①まず2次方程式を解く ②下に凸のグラフを書く ③不等号4種類から解を判断
- 2次方程式の解がない場合のみ解は2種類。他は4種類
- 上に凸のグラフは,両辺に −1 を掛けて下に凸のグラフで考えればよい
本時はグラフを活用して2次不等式の解き方について学習しました
2次不等式の解き方3ステップを活用して,考えていくようにしてくださいね!
今回は以上です。ありがとうございました
 サッカークロス
サッカークロス 

