madoryの『高校数学のブログ授業』です
- 数学を基礎から学び直したい高校生
- 高校入学前に予習して備えたい中学生
- 挫折した高校数学に再挑戦したい社会人
こんな❝あなた❞に向けて発信しています!
本時で学習するのは2次方程式です
本単元❝2次関数❞ではもちろんのこと,数学の計算における2次方程式は非常に重要な位置づけです
そんな2次方程式の解き方を整理して理解していきましょう
さっそく本時の結論です
「因数分解できなければ解の公式,xの係数が偶数ならば解の公式 part2!」
この結論にしたがって,順番に見ていきましょう
因数分解の利用
2次方程式を解く際にまず考えるのは,因数分解が利用できるかどうかです
因数分解ができれば2次方程式を解くのは容易です


2次方程式の解(答え)は基本的に2個あるよ!


2乗の形に因数分解される場合は,
本来は2個ある答えが重なって1個になる感じだね!

そうそう!
答え(解)が重なるから,重解(じゅうかい)と呼ぶこともあるよ♬


x2 の係数が1以外の場合は,
たすき掛けによる因数分解が考えられるね!
上記のように,因数分解を利用することで様々な2次方程式を解くことができます
解の公式 part1
もし,因数分解できなかったら,どのように2次方程式を解けばいいのか…
そこで解の公式の登場です!!
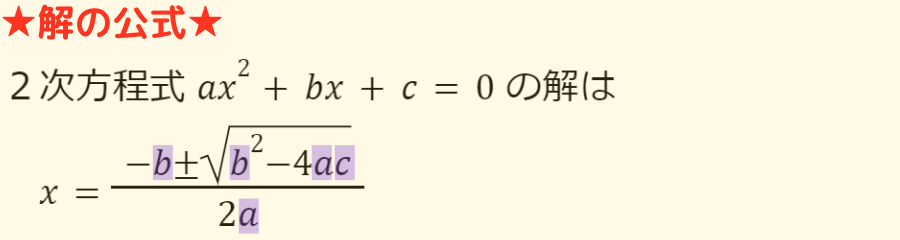
解の公式を用いた2次方程式の解き方を見てみましょう

中学校でも学習済みの解の公式は,因数分解できない2次方程式を解く際に威力を発揮します!


(5) は (3) と同じ問題だ!!

因数分解で解ける2次方程式で解の公式を使うと,
約分の手間が掛かり時間が掛かるからオススメしないよ!
解の公式 part2
解の公式には,約分の計算の手間を省くことができる ❝part2❞ が存在します
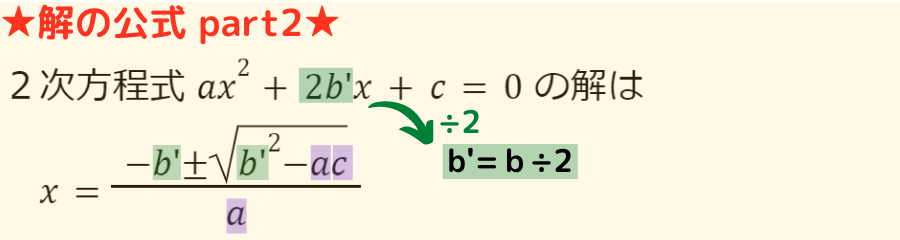
解の公式 part2 を用いた問題を見てみましょう
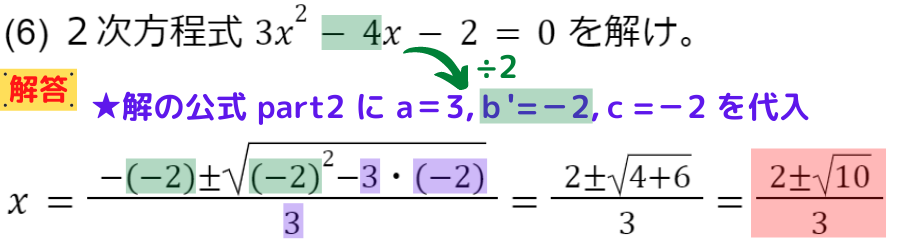

bが偶数(2で割り切れる)の場合に,
解の公式 part2 を使うといいよ♬


bに注意して解の公式 part1 か part2 か判断すればいいね♬
★補足★ bが偶数の場合に解の公式 part1 を使うと…
上記の (7) の問題を解の公式 part1 で解いた場合を見てみましょう


約分の計算の手間があるから,計算に時間が掛かるね!

その通り!!
bが偶数のときは,必ず解の公式 part2 を使うようにしたいね♬
それでは本時のまとめです
- 2次方程式を解く際にまず考えることは,因数分解が使えるかどうか
- 因数分解が使えない場合,解の公式を利用して2次方程式を解く
- xの係数であるbが偶数(2で割り切れる)の場合,解の公式 part2 を利用するとよい
- bが偶数のときに解の公式 part1 を使うと,約分の計算の手間があり計算に時間が掛かる
本時は2次方程式の解法について確認してきました
2次方程式を解く際は,まず因数分解,次に解の公式,そしてbが偶数の場合は解の公式 part2 を利用する!
このことを肝に銘じて問題を解くようにしてくださいね
今回は以上です。ありがとうございました
 サッカークロス
サッカークロス 

