madoryの『高校数学のブログ授業』です
- 数学を基礎から学び直したい高校生
- 高校入学前に予習して備えたい中学生
- 挫折した高校数学に再挑戦したい社会人
こんな❝あなた❞に向けて発信しています!
さっそく本時の結論です
「 y と f(x) は同じ意味!f(x)は代入計算を簡潔に書ける!!」
本時は2次関数の授業の初回として,今後必須となる基礎知識を紹介します
今後の学習内容をスムーズに理解できるように,新しい関数の表現方法を学びましょう
それではこの結論にしたがって,順番に見ていきましょう
関数については,中学校でも学習をしてきました
1次関数が直線のグラフ,2次関数が曲線のグラフを表しました
ここでは,関数の新しい表記とそのメリットについて考えていきましょう
関数とは?
まず,関数の定義を確認しましょう
2つの変数 x, y について,x の値が1つ決まると,それに対応して y の値がただ1つに決まるとき,y は x の関数であるという
これを聞いてピンと来るでしょうか…?いまいち分かりづらいですよね!?
そこで,もっと簡単に理解しておきましょう!
〇 x の値を代入して,y の答えが1つだったら関数である
✖ x の値を代入して,y の答えが複数あったら関数でない
答えが1つだったら関数であり,複数だったら関数でないと覚えましょう!
定義域と値域
次に,関数を考えていくうえで必要不可欠である,定義域(ていぎいき)と値域(ちいき)を紹介します
- 定義域 … x の範囲(中学校では❝ x の変域❞と学習)
- 値 域 … y の範囲(中学校では❝ y の変域❞と学習)

なんで中学校と同じように,❝変域❞を使わないのかな…??

関数の定義が「 x の値が決まる(定義する)と,y の値がただ1つに決まる」から,
x の範囲を定義域,y の範囲を値域と呼んでいるんだ!
関数 y = f(x)
これまでの関数は,必ず y = ( xの式) で表してきました
高校ではこれに加えて, f(x) = ( xの式) を使用します
y = f(x) ,つまり y と f(x) は同じ意味を表します!
関数 f(x) の値を求める


x に値を代入して計算すればいいんだね!

そうだね!
y と f(x) は同じ意味になっているんだ~。
関数 f(x) を利用した問題


条件から a と b の連立方程式になるんだね!
y を f(x) で表すメリットは?
y と f(x) が同じであることを学習しました
さて,ここで質問です!!
問「y を f(x) で表すメリットは何でしょう?」
y と f(x) ,それぞれの計算を確認し,メリットについて考えてみましょう

お分かりでしょうか?
それでは問の答えです
答「代入の計算を簡潔にまとめられること」
このようにメリットがあるので,今後は y と f(x) を使い分けていきます
最後にメリット・デメリットを整理しておきましょう
| 表記 | メリット | デメリット |
| y | アルファベット1文字で『y』と書くことができて楽 中学校までで使用しており,書き慣れている | 代入計算の際,『x=〇を代入』と書かないと伝わりづらい |
| f(x) | 代入の計算を簡潔にまとめられる | 『f』『 ()』『x』の3種類の文字と記号を書く手間が掛かる |
★補足★ 常に y = f(x)?
y と f(x) は同じ…簡単に理解できるようこのように結論づけましたが,厳密には正確ではありません
f(x) は,『 y は x の関数である』ことを表したものだからです
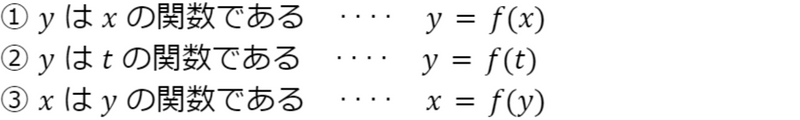

いつも y=f(x) になるわけではないんだね!
★補足★ 関数が複数になったら?


1つ目の関数は f(x),2つ目の関数は g(x)…
以下アルファベット順で f,g,h, ‥‥と表すよ!
それでは本時のまとめです
- y と f(x) は同じ意味! f(x) は代入計算を簡潔に書ける!!
- x の値が1つ決まる(定義する)と,y の値がただ1つに決まるとき,y は x の関数である
- 定義域は x の範囲( x の変域),値域は y の範囲( y の変域)
- f(1) は x=1 を代入すればよい
- y を f(x) で表すメリットは,代入の計算を簡潔にまとめられること
- y = f(x) の文字が変わることもある
- 複数の関数は f(x),g(x),h(x),‥‥ とアルファベット順に表す
本時では,関数の新しい表記を学習しました
y を f(x) で表すメリットは,代入の計算を簡潔にまとめられることでしたね!
数学を学習することで大切なのは,❝なぜ❞を追求することです
本授業で,あなたの❝なぜ❞が解決できたら嬉しい限りです♪
今回は以上です。ありがとうございました
 サッカークロス
サッカークロス 

