こんにちは,madoryです!

レッサーくん!!
『三角比の表』って見たことある?

何だろう?知らないな~。

『三角比の表』は三角比の最強ツールといえる
すばらしいものなんだ!!
本時は『三角比の表』について学習します
高校数学を勉強すると,教科書や副教材に参考書など…様々な書籍を用いることになると思います
そのどの書籍にも巻末あたりに必ず掲載されているもの…それが『三角比の表』です!!
『三角比の表』は三角比の最強ツール!
といっても過言ではありません
そんな『三角比の表』について一緒に学習していきましょう!
さっそく本時の結論です
『三角比の表』を用いて様々な長さや高さを測ることができる!
相似な図形
まず,直角三角形は角度が等しければ辺の長さの比は等しくなります
直角三角形の大きさを2倍にした図形で見ていきましょう
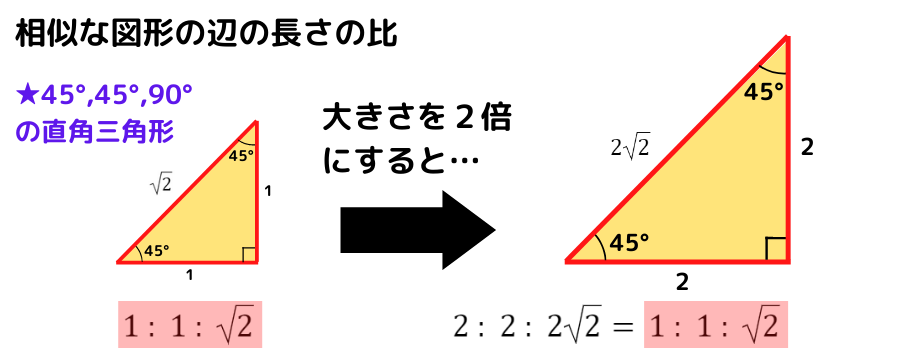

角度が一定なら辺の長さの比も常に一定になるんだね!!
上記のような,いわゆる相似比が1:2の直角三角形では,辺の長さの比は常に等しく一定であることがわかります
そして相似比が1:2に限らず,角度が一定である相似な図形であれば辺の長さの比は常に等しく一定になります

辺の長さの比が常に等しく一定になるのは,
実は直角三角形に限った話ではないんだ♬
辺の長さの比が常に等しく一定であれば,三角比の値も常に等しく一定になります
したがって,直角三角形の角度ごとの三角比の値を一覧にまとめた『三角比の表』を作ることができるわけです
三角比の表
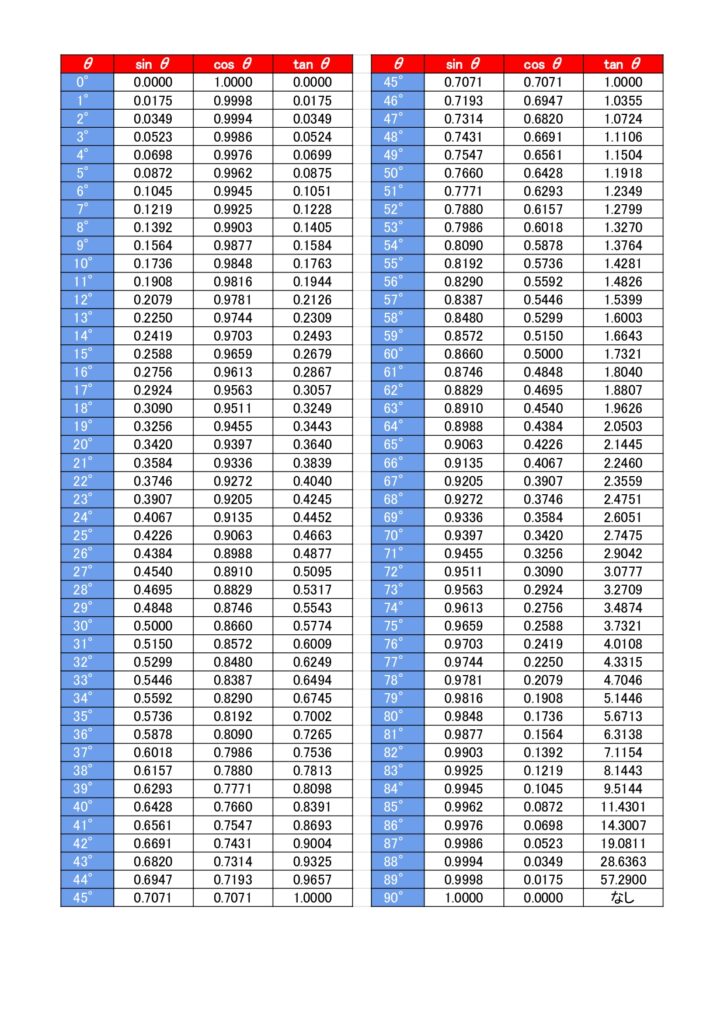
『三角比の表』は0°~90°までの三角比の値を一覧にまとめたものになります

あれ?
90°のtan(タンジェント)の値が❝なし❞になっているよ!

よく気付いたね!!
tan90°の値だけ唯一❝なし❞になるんだ。
その理由については今後学習していこうね♬
三角比の表から長さを測る①
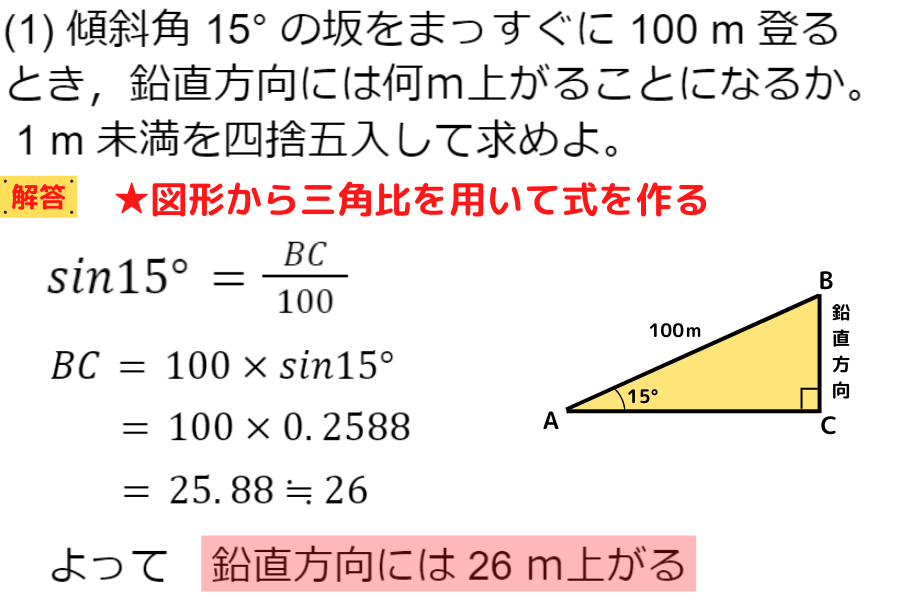

三角比の表を利用して『sin15°=0.2588』に直しているね!

この問題を別の見方をすると,
「B地点から傾斜角15°の坂を100m下ると,下った坂の高さを計算できる」
ということになるよ!
三角比の表を用いると,直角三角形の1辺と角度から,もう1辺を計算することができます
もう少し日常生活に当てはめた例を見てみましょう
三角比の表から長さを測る②
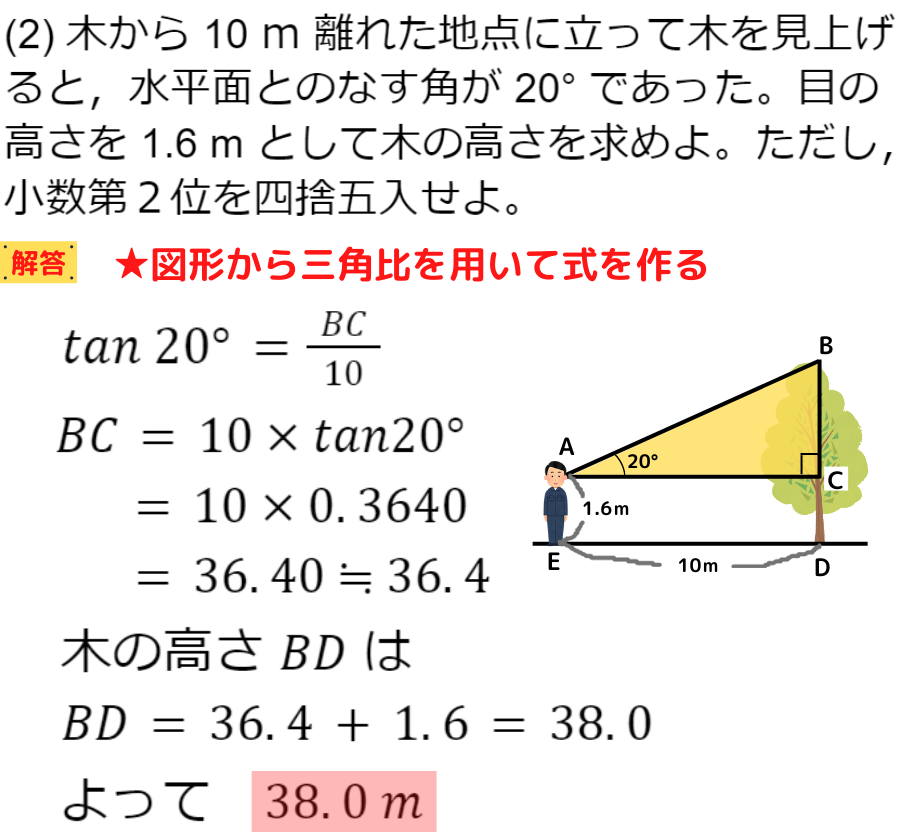

すごい!!
木の高さを計算で求めることができるんだね!

「三角比の表」が❝三角比の最強ツール❞であることが
分かってもらえたかな?

うん,分かったよ!!
「三角比の表」を使うと,いろんな長さや高さを計算できるんだね!
木の高さを測る…まさに測量ですね!
このように「三角比の表」を用いると,様々な長さや高さを計算することができます
計算の際には,『sin』『cos』『tan』のどの三角比を用いるのか,直角三角形の図から判断するようにしてください
★補足★ 測量の世界って?
現在学習中の単元名は【図形と計量】です
言葉の意味について一度整理して見ましょう
- 計量とは,長さや重さなど実際に物の量を測ること
- 測量とは,機器を用いて距離・角度・高低差を測定し,形状や面積を数値や図面で表す技術・作業の総称
『計量の一つの方法が測量』と考えると理解がしやすいでしょう
実際に街中でこのような機器を用いている人を見たことはないでしょうか?


あっ!この前見たよ!!
大人2人で道路で作業していたよ!
これは測量機を用いて,まさに❝測量❞をしている様子です
本時で学習した三角比の表の値も使用しながら,地図や図面を作成しています
❝測量❞をちょっと身近に感じませんか??
それでは本時のまとめです
- 相似な図形は辺の長さの比が等しくなるため,角度が等しければ三角比の値は常に一定
- 『三角比の表』は,直角三角形の角度ごとの三角比の値を一覧にしたもの
- 『三角比の表』には tan 90° だけ❝なし❞と記載されている
- 『三角比の表』を使うと,直角三角形の角度と1辺から,もう1辺を計算することができる
- 『三角比の表』は,長さや高さを測る❝最強ツール❞
- 単元名になっている【図形と計量】。測量は計量の一部であり,三角比の計算が用いられている
本時では,❝最強ツール❞である『三角比の表』を紹介し,実際に長さや高さを求める計算をしてきました
『三角比の表』に tan 90° だけ❝なし❞と記載されている理由は,今後のお楽しみにしてくださいね♬
本時の授業を通じて,測量を身近な存在に感じてもらえたら嬉しい限りです。
それでは今回は以上です。ありがとうございました
 サッカークロス
サッカークロス 

