サッカークロス 
madoryの『高校数学のブログ授業』です
- 数学を基礎から学び直したい高校生
- 高校入学前に予習して備えたい中学生
- 挫折した高校数学に再挑戦したい社会人
こんな❝あなた❞に向けて発信しています！
さっそく本時の結論です
「グラフの平行移動は，平方完成 or 平行移動の公式を使おう！」
グラフの平行移動の問題を解くためには，次の２種類の方法があります
- 平方完成を利用する方法
- 平行移動の公式を利用する方法
結論にしたがって，順番に見ていきましょう
平行移動とは，『平面上で図形上の各点を一定の向きに，一定の距離だけ動かすこと』を指します
少々ややこしいですので，簡単にまとめると…
グラフの平行移動とは『グラフの形を変えずに移動すること』です
平行移動の前後でグラフの形が変わらないことは，きちんと押さえておきましょうね♪
グラフの平行移動 ①平方完成の利用
平方完成の方法については，こちらの授業を参考にしてください
【２次関数④】平方完成で求める『軸と頂点』
ホッくん
平方完成を利用したグラフの❝平行移動❞の問題を見ていこう！
レッサーくん
平行移動は❝グラフの形が変わらない❞ことがポイントなんだね♬
ホッくん
下図のように，グラフで見ると平行移動はイメージしやすいよ！
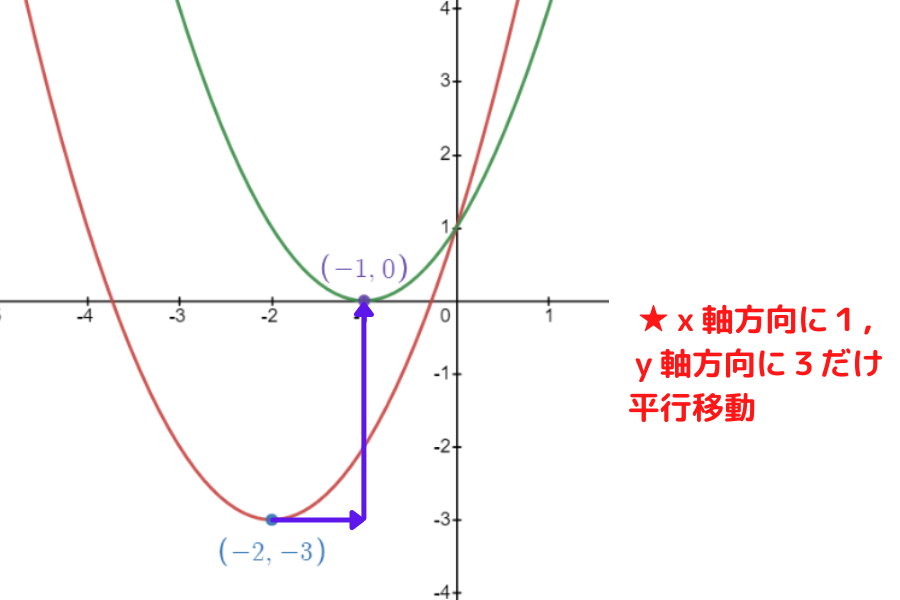
平行移動の公式
ホッくん
❝２次関数❞だけでなくどんな❝関数❞でも成り立つんだ！
今後，他の関数でも応用していく大事な公式だよ♬
グラフの平行移動 ②平行移動の公式を利用
レッサーくん
ｘ2 の係数が１以外だから，もし平方完成すると計算が大変！
公式を使うと簡単になるね♬
ホッくん
グラフだと下図のようになるよ！
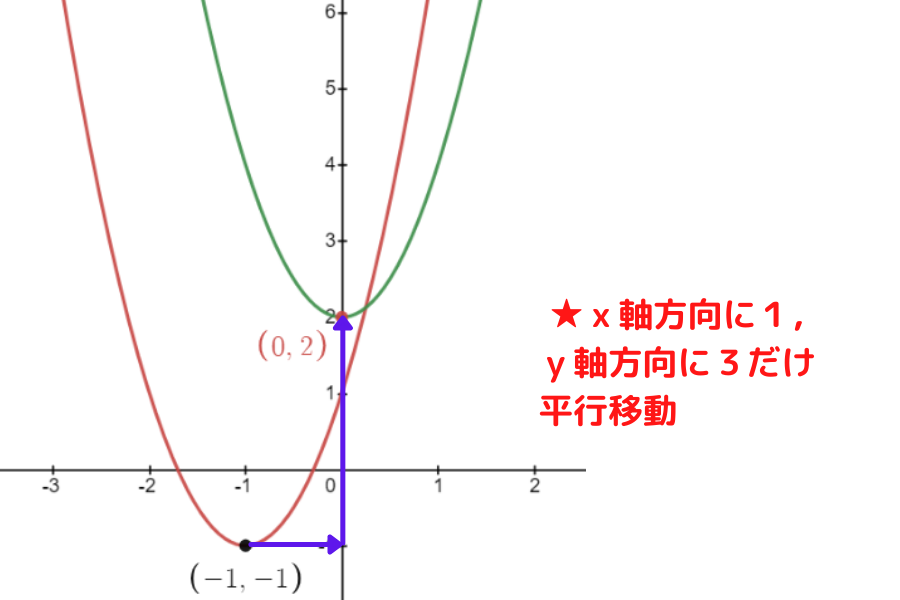
★補足★ １次関数で考える平行移動の公式
平行移動の公式は，２次関数だけでなくどんな関数においても成り立ちます
１次関数の場合の例を見てみましょう
ホッくん
直線のグラフでも下図のように平行移動が確認できるよ！
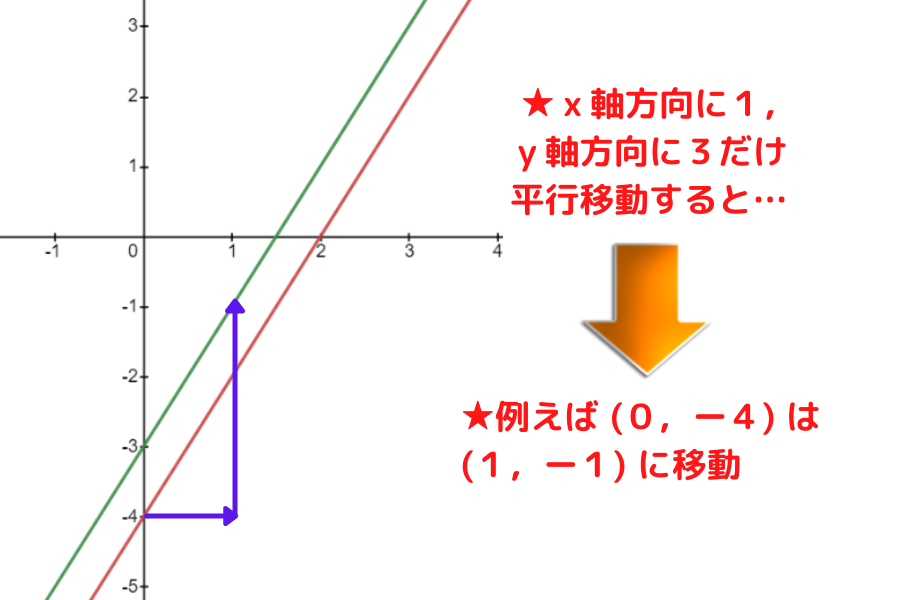
それでは本時のまとめです
- グラフの平行移動を解く方法は２つ。平方完成を利用する方法 or 平行移動の公式を利用する方法
- グラフの平行移動とは，グラフの形を変えずに移動すること
- 平方完成を利用する方法では，頂点の座標を求めてそれを移動させればよい
- 平行移動はグラフの形が変わらないため，ｘ2 の係数が変わらないことに注意
- 平行移動の公式は，移動した分をｘとｙに置き換えて代入する
- 平行移動の公式は，２次関数だけでなくどんな関数についても成り立つ
- グラフを書くと平行移動をイメージしやすい
本時では２次関数のグラフの平行移動をメインに取り扱いました
★差がつくアドバイス★
グラフの平行移動は…
① 頂点の座標を求めてそれを移動させる方法（２次関数特有の方法）
② 平行移動の公式を利用する方法（どんな関数でも成り立つ方法）
上記のように整理して使いこなしていきましょう！
今回は以上です。ありがとうございました
