
四分位数って何?

データの散らばりを見る指標のことで
3つに分かれるんだ!
ということで本時は
- データの散らばりを表す数値を理解したい
- 四分位数についてきちんと知りたい
こんなあなたに向けた内容です
四分位数はデータの分析の単元でしか学習をしないので,「あれ四分位数って何だっけ??」となりがちです
言葉の意味と求め方をしっかり理解していきましょう!
さっそく本時の結論です
範囲,四分位数,四分位範囲,四分位偏差の求め方を理解し,範囲と四分位範囲によってデータの散らばりを比較できるようにしよう!

データの散らばり

範囲
まずは範囲を紹介します
範囲とはデータの『最大値ー最小値』のことです
テストを例に挙げると『最高得点ー最低得点』で計算できます
最高得点100点・最低得点0点であれば,『100ー0=100』なので範囲は100
最高得点80点・最低得点30点であれば,『80ー30=50』なので範囲は50
となります
もう少し掘り下げて問題を見ていきましょう


散らばりの度合いが大きいということは
データがより散らばっているということだよ!
四分位数
次に四分位数(しぶんいすう)です
四分位数とは,データを値の大きさ順(小さい順)に並べたとき,4等分する位置にくる値のことです
四分位数は小さい方から順に 第1四分位数Q1,第2四分位数Q2,第3四分位数Q3 といいます

4等分して❝四つに分ける❞から❝四分❞位数と言うんだよ♬
四分位数は次の手順で求めます
- データを大きさ順(小さい順)に並べて中央値を求める(=第2四分位数Q2)
- 中央値を境界として下の組と上の組に2等分する。ただし,データが奇数個の場合は中央値はどちらの組にも含めない
- 下の組の中央値(=第1四分位数Q1)と上の組の中央値(=第3四分位数Q3)を求める
まとめると
『第1四分位数Q1=下の組の中央値』,『第2四分位数Q2=中央値』,『第3四分位数Q3=上の組の中央値』
となります
中央値については,こちらの授業で復習してください
四分位数について図で整理してみましょう
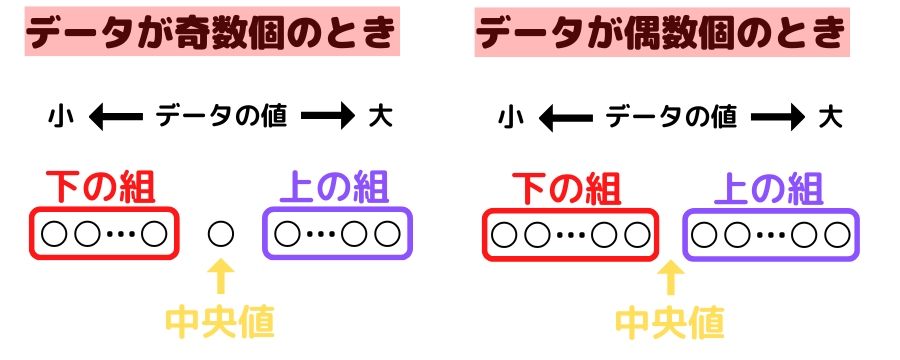

データが奇数個と偶数個で組の分け方が違うんだね!

奇数個のとき,中央値は組の中に含めないよ
例をあげて見てみましょう


四分位数が1つに定まらないときは2つの数の平均を求めるよ!
データの個数が増えても,奇数個か偶数個か見極められればOKです
このように,普通の中央値はデータを2分割,四分位数はデータを4分割にしています
さらに中央値を細かくしたのが四分位数とも言えますね!
四分位範囲と四分位偏差
次に四分位範囲(しぶんいはんい)と四分位偏差(しぶんいへんさ)を紹介します
四分位範囲とは『第3四分位数Q3ー第1四分位数Q1』のことです
そして四分位偏差とは『四分位範囲 ÷2』です

範囲と四分位範囲って似ていてまぎらわしいね…

四分位範囲は❝四分位数の❞『最大値ー最小値』と考えるといいよ♬
範囲とは『最大値ー最小値』のことでしたね
四分位範囲を❝四分位数の❞『最大値ー最小値』と考えると理解しやすいのでオススメです!
四分位偏差は四分位範囲を求めて❝2❞で割るだけなので簡単です
問題を見てみましょう


四分位範囲でもデータの散らばりが分かるんだね
四分位数を求められれば,四分位範囲によってデータの散らばりを比較できるようになります
単純に四分位範囲が大きい方がデータがより散らばっていると判断します
★補足★ 範囲と四分位範囲ってどう使い分ける?

あれ…範囲と四分位範囲はどう使い分けるの?

それぞれの特徴を比べてみようか
データの散らばりを比較する指標として,範囲と四分位範囲を紹介しました
さて,この2つはどう使い分ければいいのでしょうか?
範囲と四分位範囲の特徴を比較してみましょう
①範囲は『最大値ー最小値』で,四分位範囲は『第3四分位数Q3ー第1四分位数Q1』なので❝四分位数の❞『最大値ー最小値』といえる
②範囲はデータの100%すべての散らばりを計算し,四分位範囲はデータの中央50%の散らばりを計算している
③範囲はすべてのデータを基に計算していると言えるが,極端にかけ離れたデータの影響を受けやすい
④四分位範囲はすべてのデータを基に計算していると言えないが,極端にかけ離れたデータの影響を受けにくい
すべてのデータを利用して計算していることから範囲の方がよい…とも言えそうですが,範囲はかけ離れたデータの影響を受けやすい特徴があります
極端な例で考えてみると
「テストで50点を取ったのが4人,0点と100点が1人ずつの場合」
つまり
「0,50,50,50,50,100」
のデータで範囲と四分位範囲を考えてみましょう
範囲は『100ー0=100(点)』,四分位範囲は『50ー50=0(点)』となります
この場合,範囲は極端にかけ離れたデータの影響を受けるため,データの散らばりを比較するのに範囲でなく四分位範囲を用いた方が良いのでは…となりますよね!

極端にかけ離れたデータがなければ範囲,
あれば四分位範囲が有効と言えるね!

【まとめ】範囲でデータの100%,四分位範囲でデータの中央50%の分析をしよう!

それでは本時のまとめです
- 範囲は『最大値ー最小値』で求められる
- 四分位数はデータを小さい順に並べて4分割し,その境目を順に第1四分位数Q1・第2四分位数Q2・第3四分位数Q3 という
- 四分位範囲は『第3四分位数Q3ー第1四分位数Q1』で求められる
- 範囲と四分位範囲によってデータの散らばりが比較できる
- 範囲はデータの100%すべて,四分位範囲はデータの中央50%の散らばりを比較している
- 範囲は極端にかけ離れたデータの影響を受けやすいと言える
本時は四分位数について紹介し,範囲と四分位範囲によってデータの散らばりを比較してきました
「どちらのデータの方が散らばっているの?」
この問いに対する答えは必ずしも1つではありません
使う指標が範囲か四分位範囲かによって,データの散らばりの度合は異なるケースがあります
両方の特徴を踏まえて,どちらの指標でデータの散らばりを比較するのか判断してくださいね!
今回は以上です。ありがとうございました
 サッカークロス
サッカークロス 

